The problem

Given two audio recordings, identify whether they correspond to the same audio content .

Audio representation

Audio representation

Audio representation

Audio representation

Fingerprinting audio tracks

Fingerprinting audio tracks

Case study: Shazam (2003)

Fingerprinting audio tracks

Case study: Shazam (2003)

• Finding peaks: Identify local maxima in the spectrogram.
  For every $n,m$, compare $\widehat{S}(n,m)$ with the average of intensities in a neighborhood $\mathcal{N}(n,m)$.
  Identify $(n,m)$ such that $\widehat{S}(n,m)>\sum_{(n',m')\in \mathcal{N}(n,m)} \widehat{S}(n',m')$.

Comparing audio tracks

Case study: Shazam (2003)

• Matching: Given two tracks, match pairs of hashes that coindide.

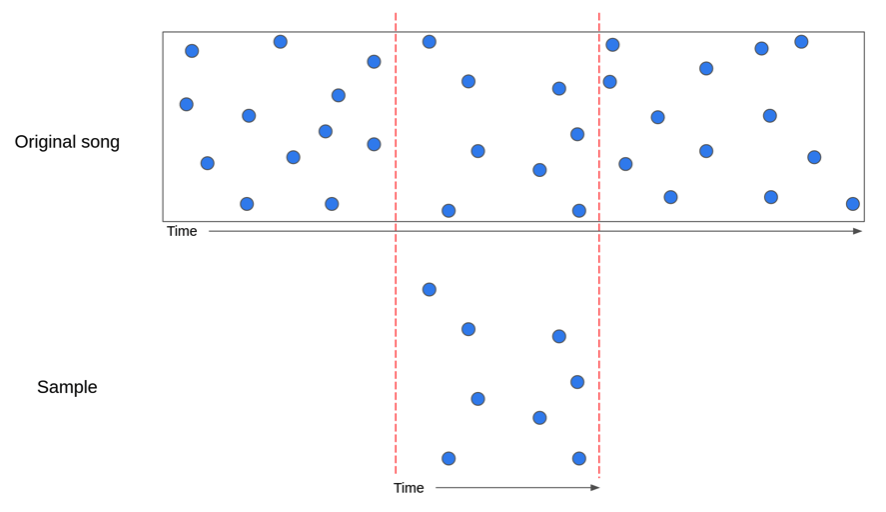
Comparing audio tracks

Case study: Shazam (2003)

• Scoring: Compute the histogram of time difference for every matched pair of hashes. The score of a matching is the size of the largest bar.

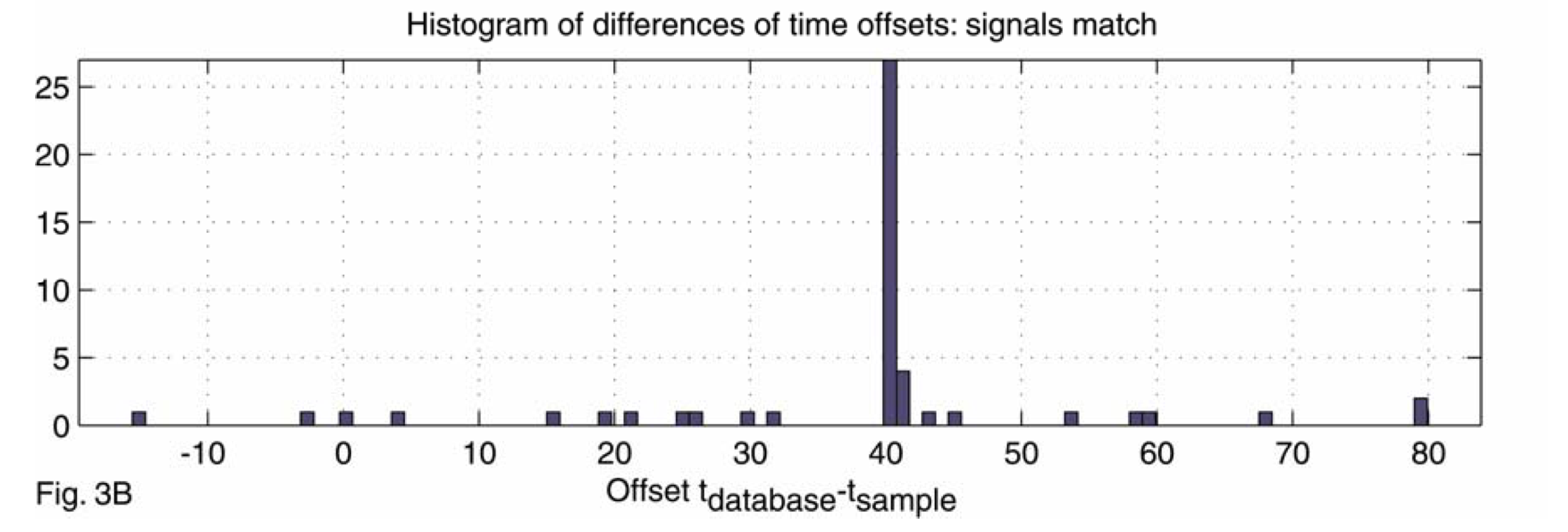
Obfuscations of Audio tracks

• Original track
  
• Addition of noise
  
• Reverberation
  
• Low/High pass filter
  
• Tempo shift
  
• Pitch shift
  

Obfuscations of Audio tracks

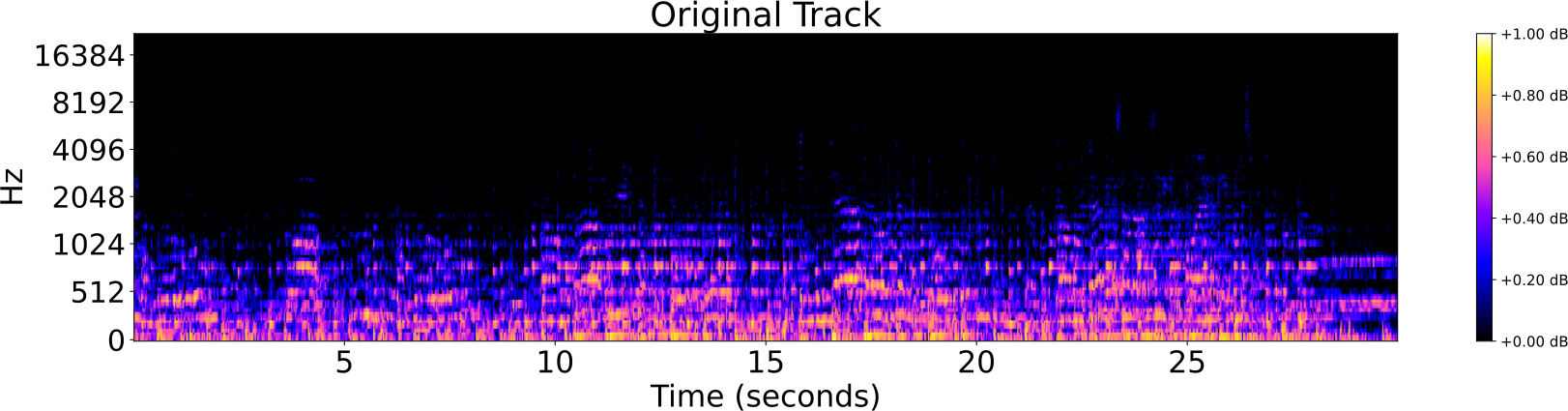
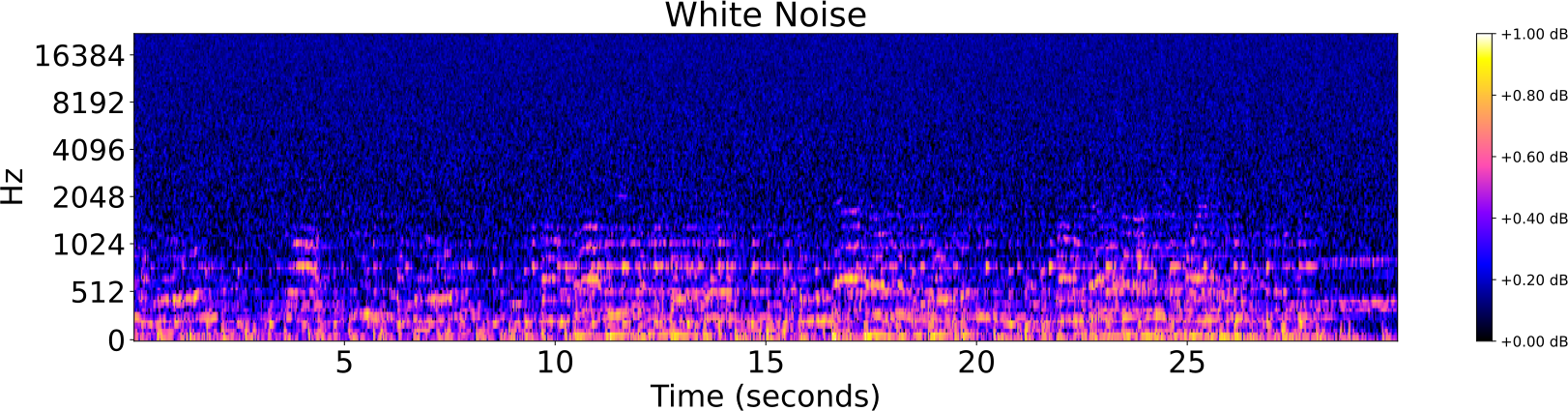
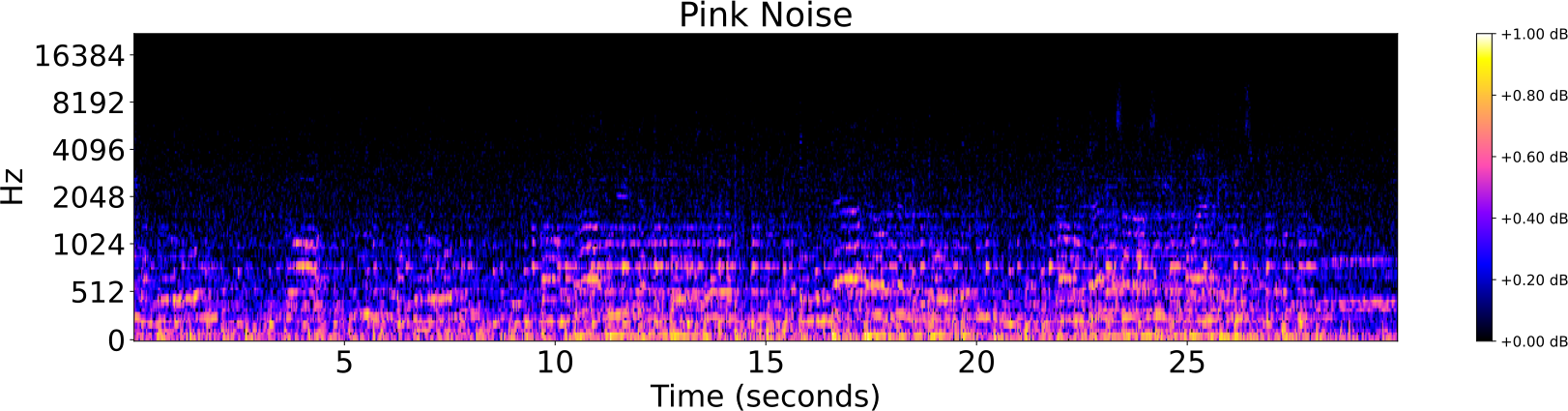
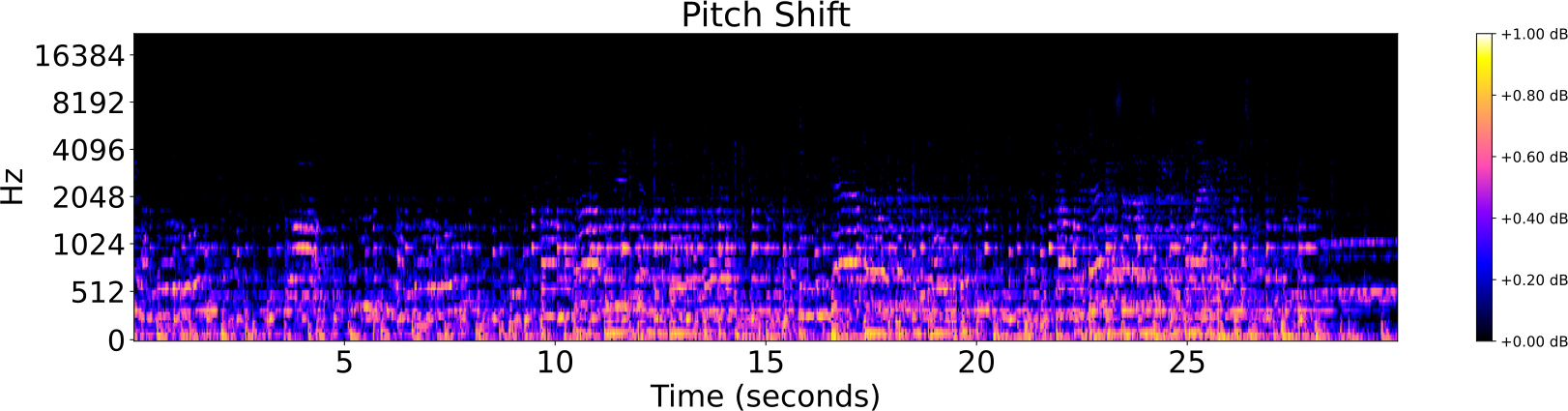
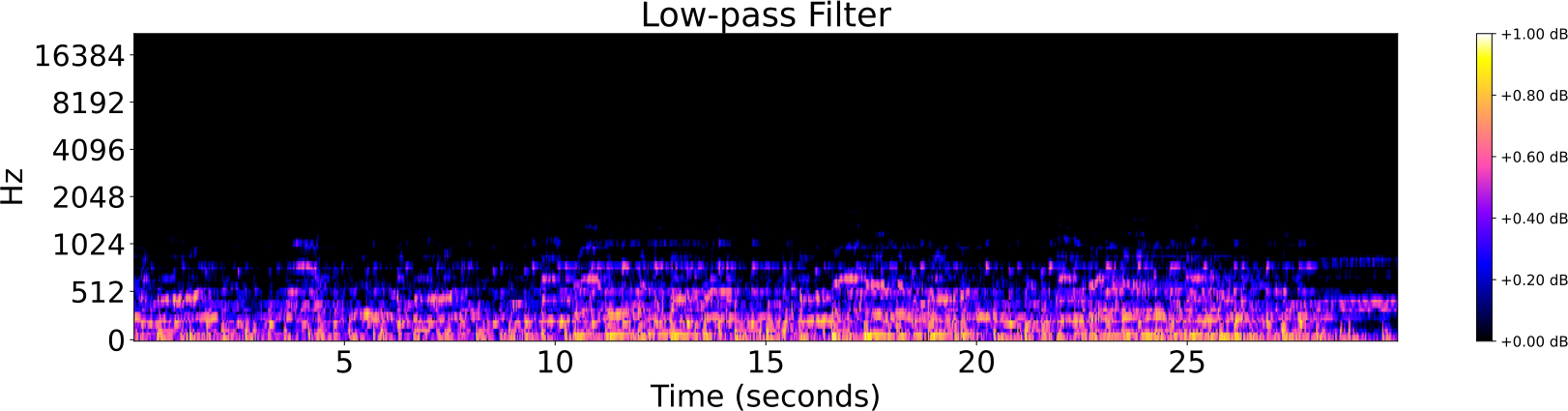
Audio Identification

Case study: Shazam

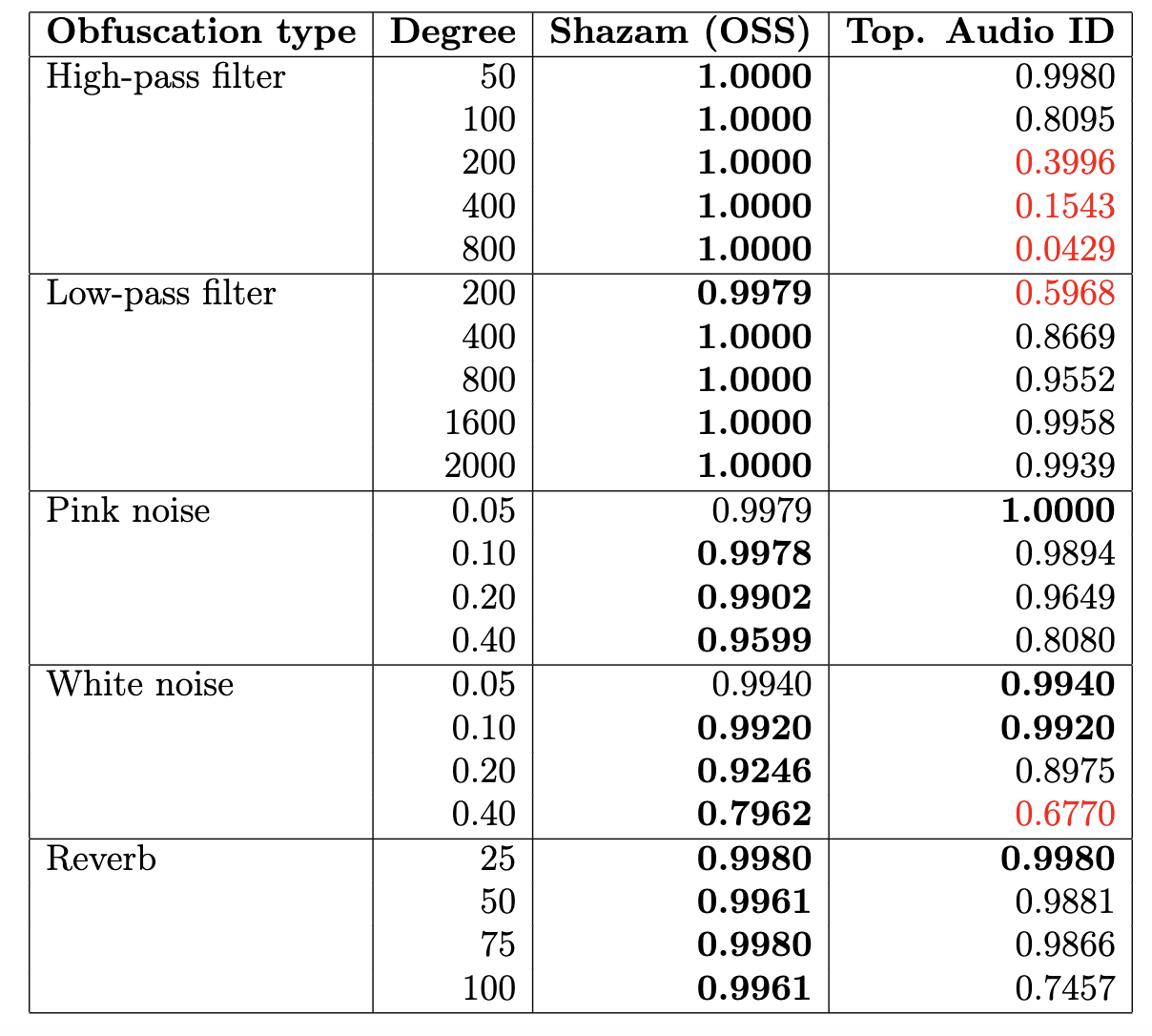
• The algorithm has good performance for rigid obfuscations of audio tracks, such as:
  • addition of noise,
  • highpass/lowpass filter,
  • reverberation.


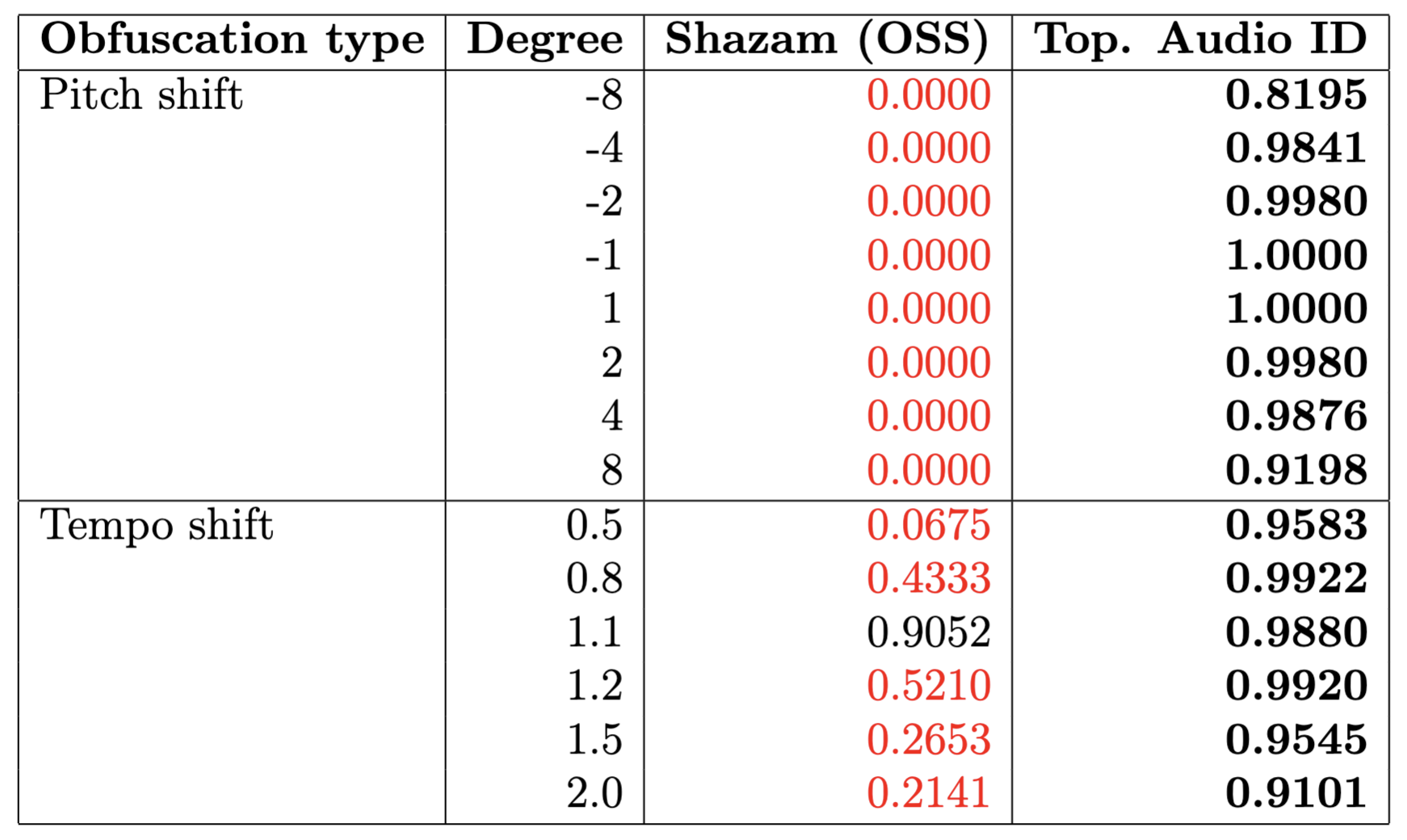
• The algorithm has poor performance for topological obfuscations of audio tracks, such as:
  • change of pitch,
  • change of tempo,
  • mixed distortions; e.g. Music Obfuscator by Ben Grosser (2015).
    

Topological
Audio Identification

Topology of spectrograms

Topology of spectrograms

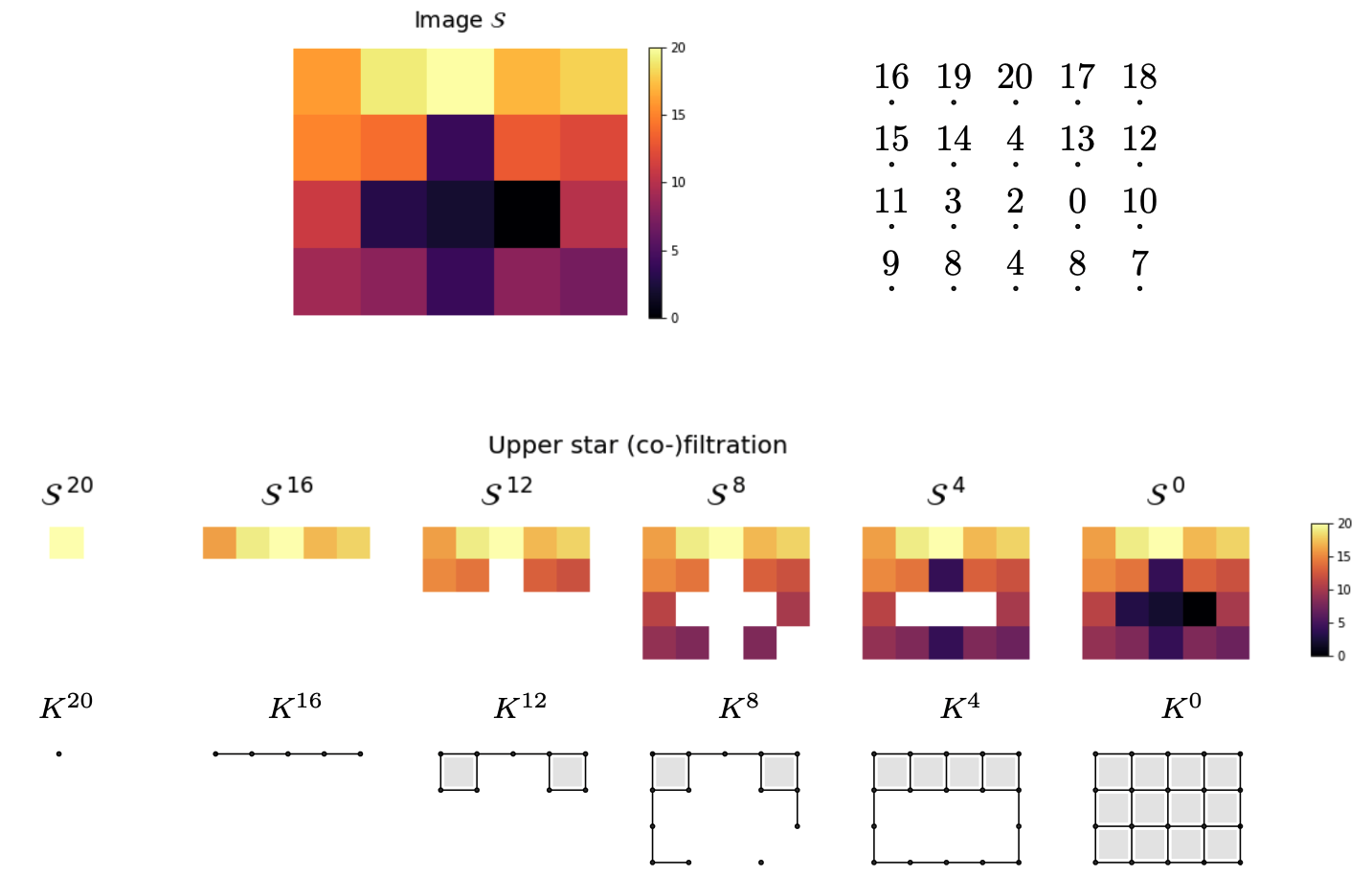
Topology of spectrograms

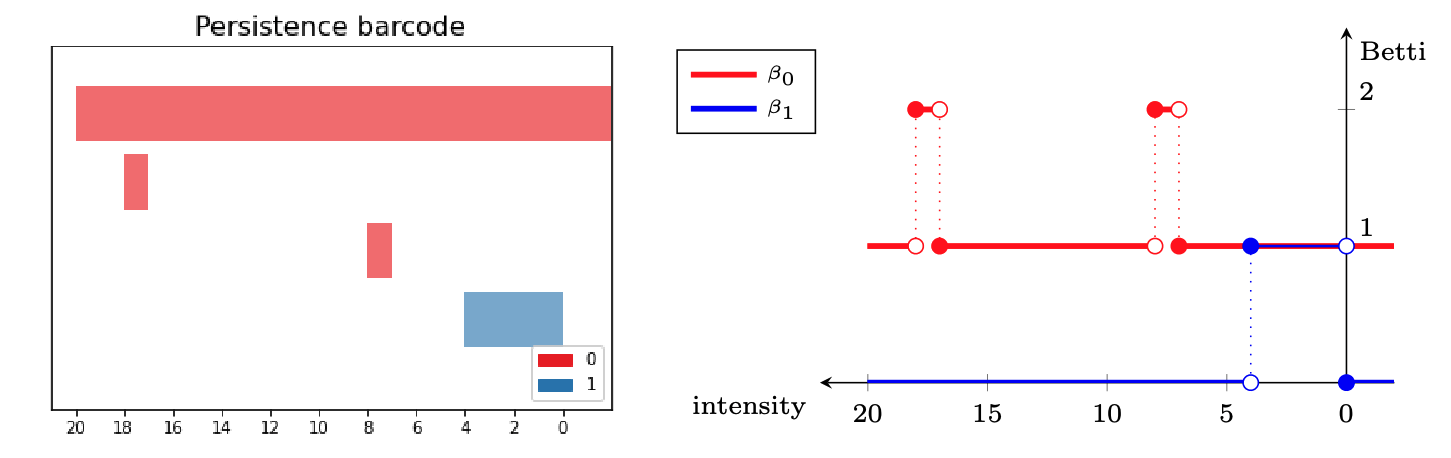
Topological fingerprints

Topological fingerprints

Let $\mathcal S$ denote the mel-spectrogram of an audio track $s:[0,T]\to \mathbb{R}$.

• Local spectral decompositions: Given $\omega$ a window size and $0<\tau<1$ an overlap constant, we subdivide $\mathcal S$ into a set of $\tau$-overlapping windows $W_0, W_1, \dots, W_k$ of $\omega$ seconds duration. We normalize the range of every window as $\frac{W_i-\min(W_i)}{\max(W_i)-\min(W_i)}.$ Let $t_i$ be the mid-time point of $W_i$.

Topological fingerprints

Let $\mathcal S$ denote the mel-spectrogram of an audio track $s:[0,T]\to \mathbb{R}$.

• Local persistence signatures: For each (normalized) window $W_i$, we compute the persistent homology of the associated upper-filtered cubical complex for dimensions 0 and 1.
  We encode the persistent barcodes as a family of Betti curves $\{\beta_{i,0}\}_{i=0}^{k}$ and $\{\beta_{i,1}\}_{i=0}^{k}$ for dimensions 0 and 1, respectively.

Topological fingerprints

Let $\mathcal S$ denote the mel-spectrogram of an audio track $s:[0,T]\to \mathbb{R}$.

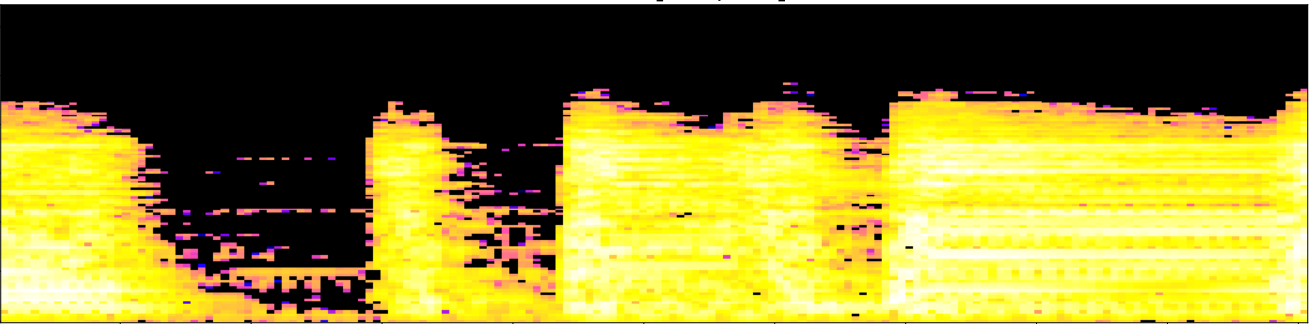
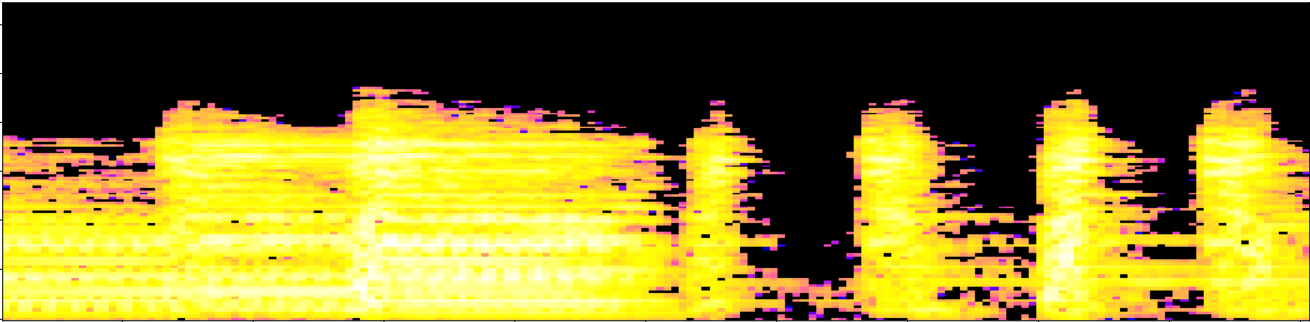
• Fingerprint: The topological fingerprint of the audio track $s$ with the resolution given by the parameters $\omega$ and $\tau$ is defined as the set of triples ${(t_i, \beta_{i,0}, \beta_{i,1})}_{i=0}^{k}$.


$~~~~~~~~~~~~t_0~~~~~~~~~~~~~~~~~~~~~~~t_1~~~~~~~~~~~~~~~~~~~~t_2~~~~~~~~~~~~~~~~~~~~~t_3~~~~~~~~~~~~~~~~~~~~~~t_4~~~~~~~~~~~~~~~~~~~~~t_5 \dots$

Comparing fingerprints

Comparing fingerprints

• Distance: Let $s$, $s'$ be two audio tracks and let ${(t_i, \beta_{i,0}, \beta_{i,1})}_{i=0}^{k}, {(t_j', \beta'_{j,0}, \beta'_{j,1})}_{j=0}^{k'}$ be its associated fingerprints.

$~~~~$

$~~~~~~~~~~~~~~~~t_0~~~~~~~~~~~~~~~~t_1~~~~~~~~~~~~~~~~t_2~~~~~~~~~~~~~~~t_3~~~~~~~~~~~~~~~t_4~~\dots~~~~~~~~~~~~~~~~~~t'_0~~~~~~~~~~~~~~~~t'_1~~~~~~~~~~~~~~~~t'_2~~~~~~~~~~~~~~~~t'_3~~~~~~~~~~~~~~~t'_4~~\dots$

Comparing fingerprints

• Distance: Let $s$, $s'$ be two audio tracks and let ${(t_i, \beta_{i,0}, \beta_{i,1})}_{i=0}^{k}, {(t_j', \beta'_{j,0}, \beta'_{j,1})}_{j=0}^{k'}$ be its associated fingerprints.

For every homological dimension $d=0,1$, the $d$-Betti distance matrix $M_d$ between $s$ and $s'$ is defined as $$(M_d)_{i,j} = \Vert \beta_{i,d} - \beta'_{j,d} \Vert_{L^1}.$$

We summarize the distance between every pair of windows $W_i$ and $W_j'$ as $$C_{i,j} = \lambda (M_0)_{i,j} + (1-\lambda) (M_1)_{i,j}$$ for a parameter $0\leq \lambda\leq 1$.

Comparing fingerprints

• Matching: We compare $s$ and $s'$ via a minimum-cost matching in $C$.

Comparing fingerprints

• Matching: We compare $s$ and $s'$ via a minimum-cost matching in $C$.

Comparing fingerprints

• Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.

Comparing fingerprints

• Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.

For $m\geq 1$, compute $\bar t'_{j_i} = \mathrm{median} \{t_{j_{i-m}},\dots, t_{j_{i-1}}, t_{j_i}, t_{j_{i+1}}, \dots, t_{j_{i+m}}\}$, the moving median at $t_{j_i}$. Consider $\bar P=\{( t_{i}, \bar t_{j_i}'): i =1,\dots,k\}$.

Comparing fingerprints

• Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.

For $m\geq 1$, compute $\bar t'_{j_i} = \mathrm{median} \{t_{j_{i-m}}, t_{j_{i-m+1}}, \dots, t_{j_{i-1}}, t_{j_i}\}$, the moving median at $t_{j_i}$. Consider $\bar P=\{( t_{i}, \bar t_{j_i}'): i =1,\dots,k\}$.

We assess the functional increasing dependency of the points in $P$ as $$\rho_{\bar P} = \mathrm{Pearson}\{(t_i), (\bar{t}'_{j_i})\}.$$

Comparing fingerprints

• Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.

For $m\geq 1$, compute $\bar t'_{j_i} = \mathrm{median} \{t_{j_{i-m}}, t_{j_{i-m+1}}, \dots, t_{j_{i-1}}, t_{j_i}\}$, the moving median at $t_{j_i}$. Consider $\bar P=\{( t_{i}, \bar t_{j_i}'): i =1,\dots,k\}$.

We assess the functional increasing dependency of the points in $P$ as $$\rho_{\bar P} = \mathrm{Pearson}\{(t_i), (\bar{t}'_{j_i})\}.$$

Experimental Results

Experimental Results

Music Obfuscator by Ben Grosser

Experimental Results

Music Obfuscator by Ben Grosser

Experimental Results

Spotify Database + PySOX Transformer

• Spotify Web API. Dataset of 30 seconds preview snippets of (~135.000) songs.


• PySOX Transformer. Every audio track has been then manipulated according to seven types of obfuscations in a range of different degrees of magnitude.

Obfuscation type	Degree
Low Pass Filter	200, 400, 800, 1600, 2000
High Pass Filter	50, 100, 200, 400, 800, 1200
White Noise	0.05, 0.10, 1.20, 0.40
Pink Noise	0.05, 0.10, 1.20, 0.40
Reverberation	25, 50, 75, 100
Tempo	0.50, 0.80, 1.1 1.2, 1.50, 2.00
Pitch	-8, -4, -2, -1, 1, 2, 4, 8



• Positive and negative pairs. For every obfuscation type and degree, we generated a random set of 1000 positive pairs (36000 in total). We also generated a random set of 36000 negative pairs.

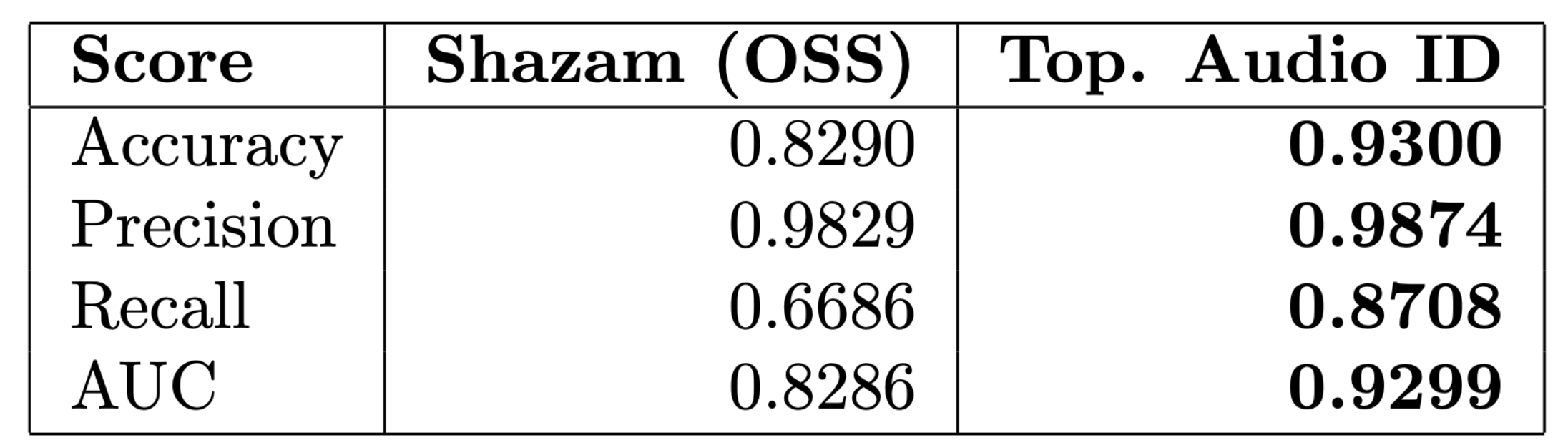
Experimental Results

(Accuracy)

Rigid distortions

Topological distortions

What I Learned

UnMet Needs: Industry Applications of TDA

What I Learned

UnMet Needs: Industry Applications of TDA

What I Learned

UnMet Needs: Industry Applications of TDA

What I Learned

UnMet Needs: Industry Applications of TDA

What I Learned

UnMet Needs: Industry Applications of TDA

What I Learned

UnMet Needs: Industry Applications of TDA

What I Learned

UnMet Needs: Industry Applications of TDA

References