Coloquio Departamento de Matemática, FCEyN, UBA
Let it Be(tti):
Huellas topologicas para identificacion de audio
XIMENA FERNANDEZ
Trabajo en colaboracion con
W. REISE (Paris-Saclay), M. DOMINGUEZ, M. BEGUERISSE-DIAZ (Spotify) & H. A. HARRINGTON (Oxford).
Topological data analysis
Topological data analysis
Martin et al. Topology of cyclo-octane energy landscape. J Chem Phys. 2010
Barbensi et al. A topological eslection of folding Pathways from native states of knotted proteins. Symm. 2021

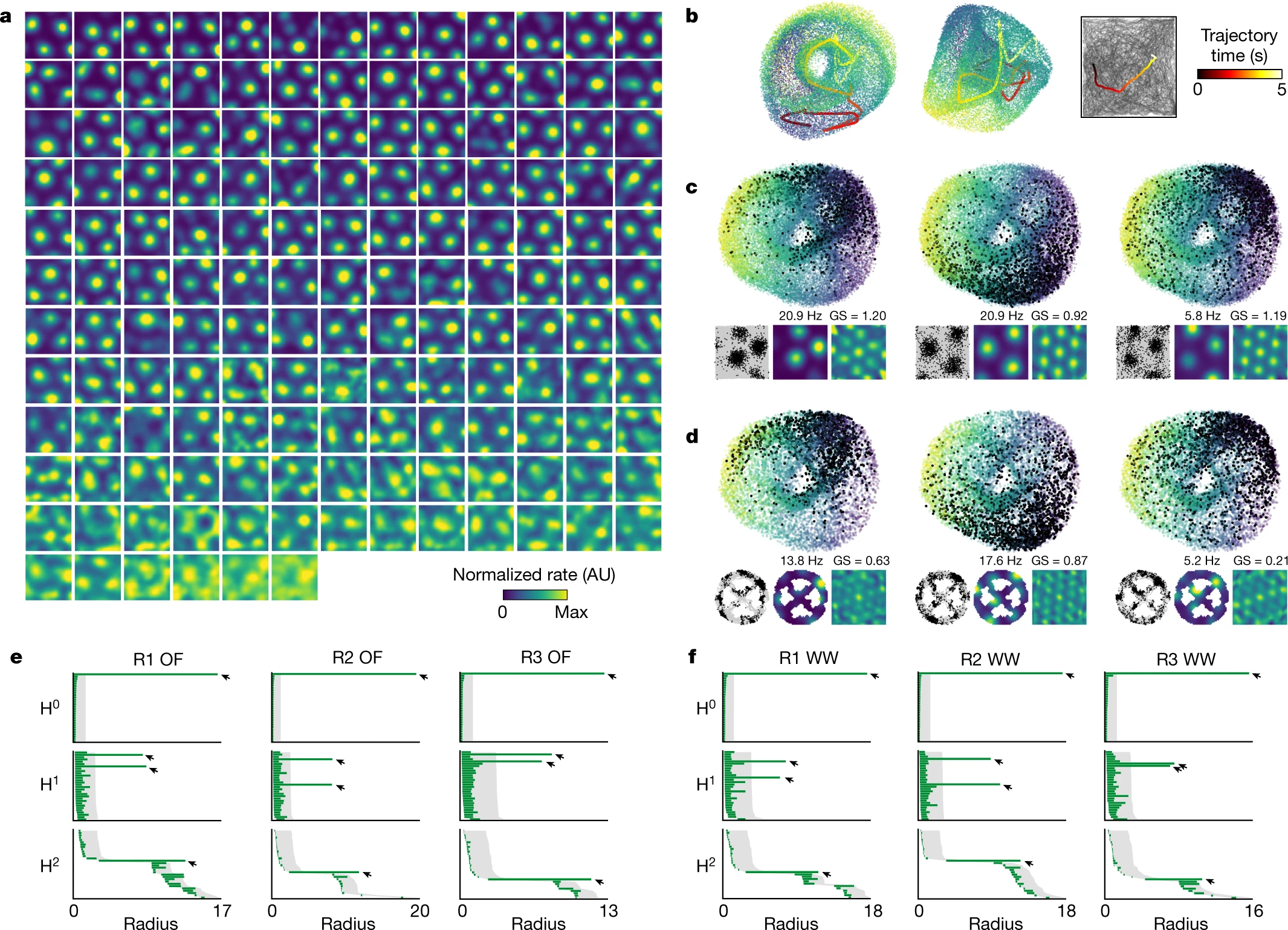
Gardner et al. Toroidal topology of population activity in grid cells. Nature. 2022
Topological data analysis
Estimation of connected components.

Carlsson, Memoli. Characterization, Stability and Convergence of Hierarchical Clustering Methods. JMLR (2010)
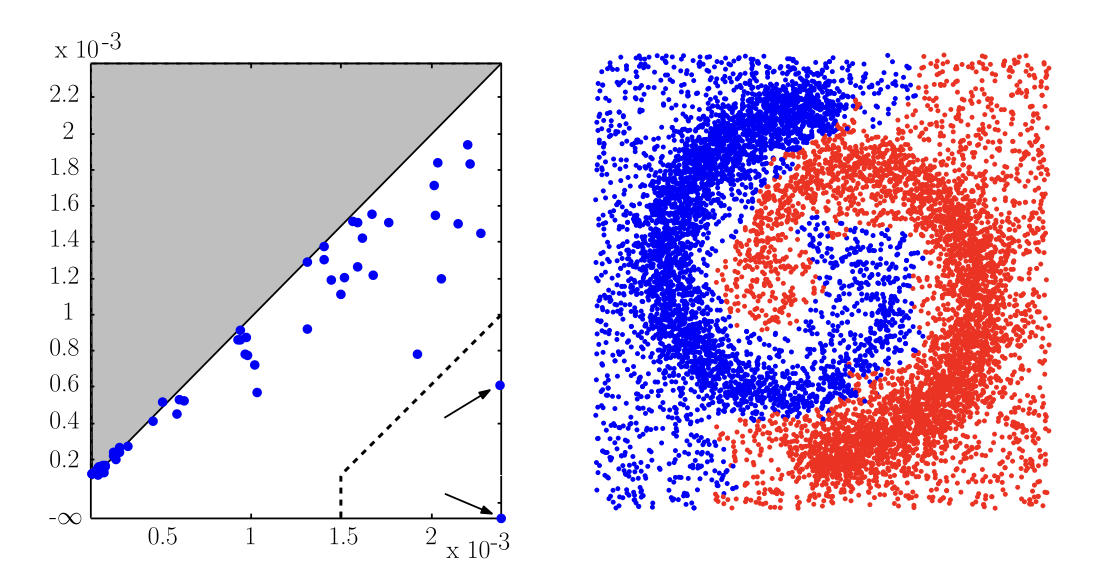
Chazal, Guibas, Oudot, Skraba. Persistence-Based Clustering in Riemannian Manifolds. Journal of the ACM (2011)

McInnes, Healy, Melville. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. Journal of the Open Source Software (2018)

Singh, Memoli, Carlsson. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition (Mapper). (2007)
Zomorodian, Carlsson. Computing Persistent Homology Discrete and Computational Geometry (2005)
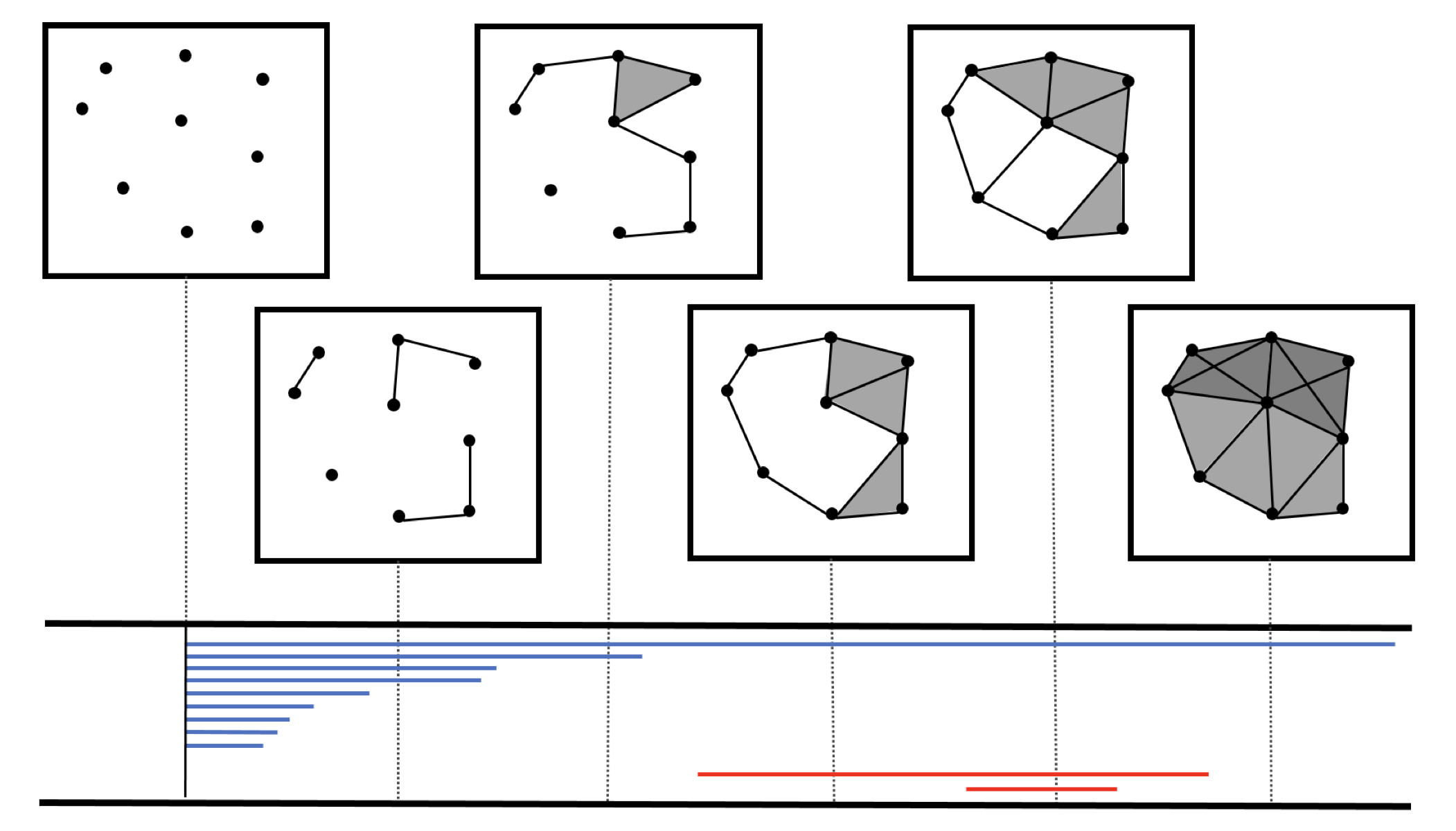
Persistent homology
Input dataset $X$.
- Combinatorics: construct an increasing family $\{X_t\}$ of complexes around $X$, where the indexing $t$ is a scale parameter in $\mathbb R\geq 0$.
- Algebraic topology: compute the $d$-th homology vector spaces $H_d(X_t)$ for scales $t\in R_{\geq 0}$ and dimensions $d \in Z_{\geq 0}$.
- Representation theory: decompose each family of vector spaces $\{H_d(X_t)\colon t \geq 0\}$ into irreducible summands, thus producing a barcode.
Source: Ali et.al. (2023)
Persistent homology
- Statistics:
- Stability: Persistence barcodes are stable with respect to perturbations of data.

Persistent homology
- Statistics:
- Stability: Persistence barcodes are stable with respect to perturbations of data.
Persistent homology
- Statistics:
- Stability: Persistence barcodes are stable with respect to perturbations of data.
- Convergence: Persistence barcodes converge to a limit barcode of the underltying space as the size of the sample $X$ goes to $\infty$.

Applications of persistence
Gardner et al. 'Toroidal topology of population activity in grid cells'. Nature. (2022)
-
L. Polterovich et.al. 'Topological persistence in geometry and analysis'. American Mathematical Society. (2020)
E. Shelukhin. 'On the Hofer-Zehnder conjecture'.
Annals of Mathematics. (2022)
Applications of persistence
Gardner et al. 'Toroidal topology of population activity in grid cells'. Nature. (2022)
$\dots$
-
Reise, Fernandez, Dominguez, Harrington, Beguerisse-Diaz. 'Topological fingerprints for audio identification'. SIAM Journal of Data Science (accepted) (2023)
-
L. Polterovich et.al. 'Topological persistence in geometry and analysis'. American Mathematical Society. (2020)
E. Shelukhin. 'On the Hofer-Zehnder conjecture'.
Annals of Mathematics. (2022)
$\dots$
Audio Identification
Audio Identification
Do you recognize this song?
Source: Music Obfuscator by Ben Grosser (2015)
Audio Identification
Given two audio recordings, identify whether they correspond to the same audio content .
The problem
Given two audio recordings, identify whether they correspond to the same audio content .
- 'Morning Song' by Le Loup:
- 'Morning Song' by Le Loup with addition of white noise:
- 'Morning Song' by Le Loup with change of tempo:
- 'Morning Song' by Le Loup with change of pitch:
Audio representation
Audio representation
- Waveform: A continuous function $s\colon\lbrack 0,T\rbrack \to \mathbb{R}$.
Audio representation
- Waveform: A continuous function $s\colon\lbrack 0,T\rbrack \to \mathbb{R}$.
Audio representation
-
(Discrete) Short-time Fourier transform: Given equally-spaced time samples of the signal $(s_n)_{n=1}^{N}$ in $\lbrack 0,T\rbrack$ and a discretization of the frequency range $\{f_m\}_{m=1}^M$, the magnitude of the frequency $f_m$
around $t_n$
is given by
\[
\widehat{S} (n,
m) = \sum_{k=-\infty}^\infty s_k \omega_{k-n}\exp\left(-i k f_m\right),
\]
where $(\omega_k)_k$ is a discrete version of a window function.
Audio representation
Fingerprinting audio tracks
Fingerprinting audio tracks
Case study:
![]() Shazam (2003)
Shazam (2003)

Fingerprinting audio tracks
Case study:
![]() Shazam (2003)
Shazam (2003)
- Finding peaks: Identify local maxima in the spectrogram.
For every $n,m$, compare $\widehat{S}(n,m)$ with the average of intensities in a neighborhood $\mathcal{N}(n,m)$.
Identify $(n,m)$ such that $ \widehat{S}(n,m)>\sum_{(n',m')\in \mathcal{N}(n,m)} \widehat{S}(n',m')$.


Fingerprinting audio tracks
Case study:
![]() Shazam (2003)
Shazam (2003)
- Fingerprint: For every peak (anchor point) $P$ at time $t_P$ and every peak $Q$ in the target zone at time $t_Q$ compute $(f_P, f_Q, t_Q-t_P)$.

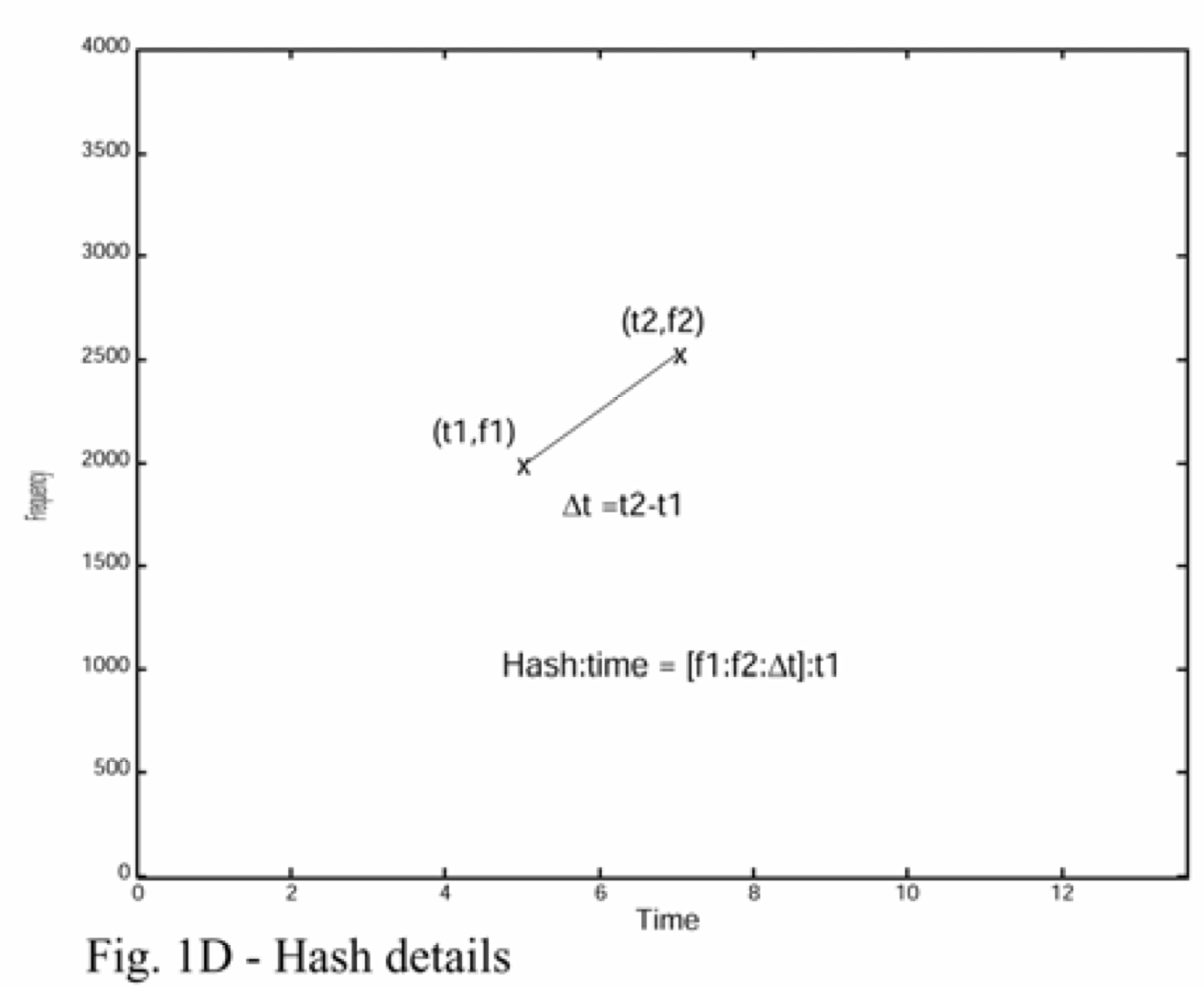
Comparing audio tracks
Comparing audio tracks
Case study:
![]() Shazam (2003)
Shazam (2003)
- Matching: Given two tracks, match pairs of hashes that coindide.
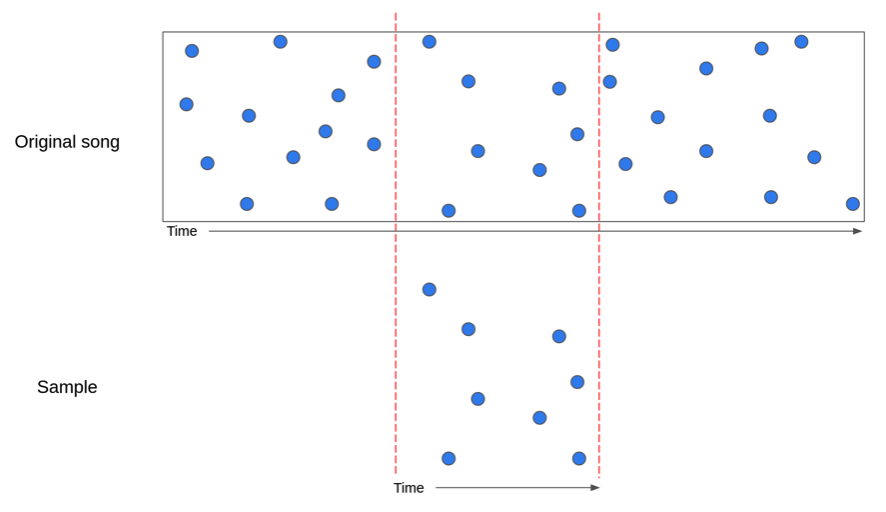

Comparing audio tracks
Case study:
![]() Shazam (2003)
Shazam (2003)
- Scoring: Compute the histogram of $t_P-t_{P'}$ for every matched pair of hashes $(f_P, f_Q, t_Q-t_P)$ and $(f_{P'}, f_{Q'}, t_{Q'}-t_{P'})$. The score of a matching is the size of the largest bar.
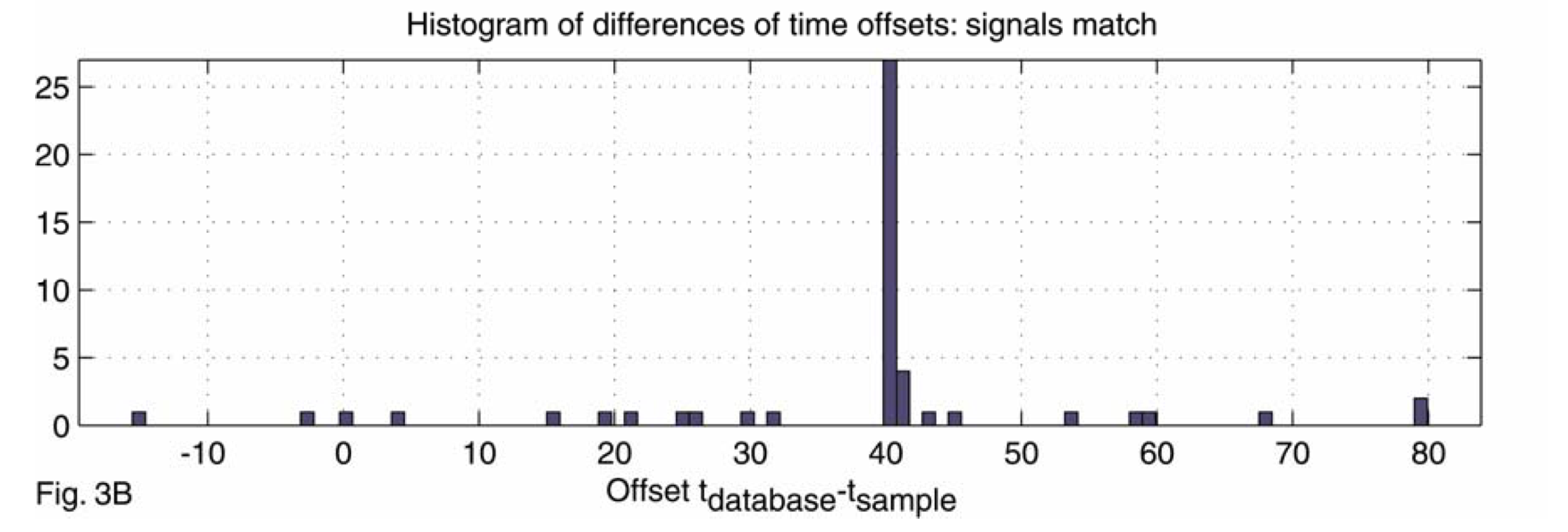
Comparing audio tracks
Case study:
![]() Shazam (2003)
Shazam (2003)
- Scoring: Compute the histogram of $t_P-t_{P'}$ for the every paired hashes $(f_P, f_Q, t_Q-t_P)$ and $(f_{P'}, f_{Q'}, t_{Q'}-t_{P'})$ in the matching. The score of a matching is the size of the largest bar.

Obfuscations of Audio tracks
- Addition of noise
- Reverberation
- Low/High pass filter
- Tempo shift
- Pitch shift
Obfuscations of Audio tracks

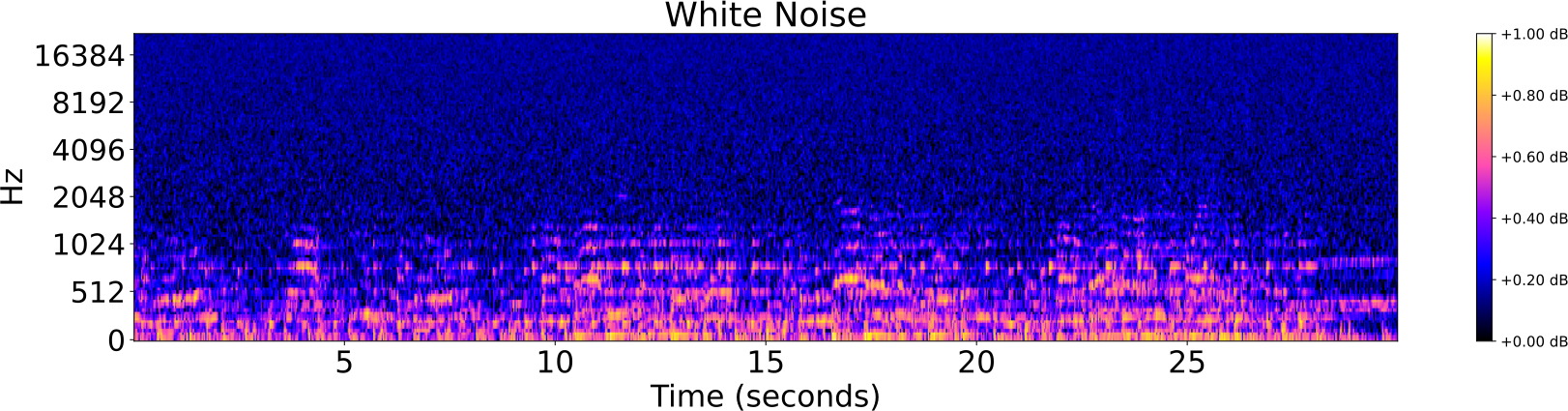
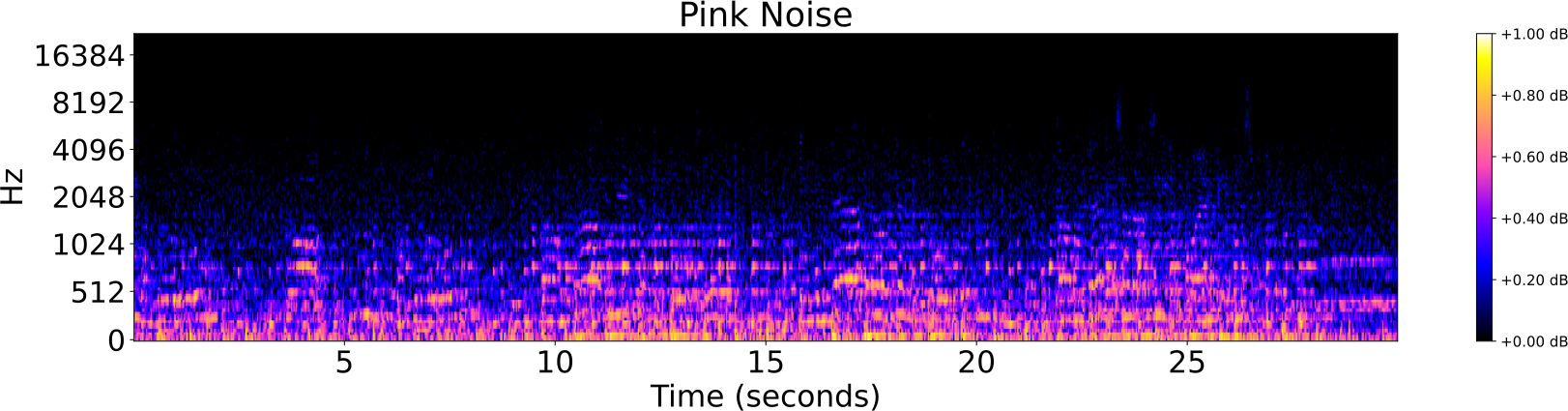

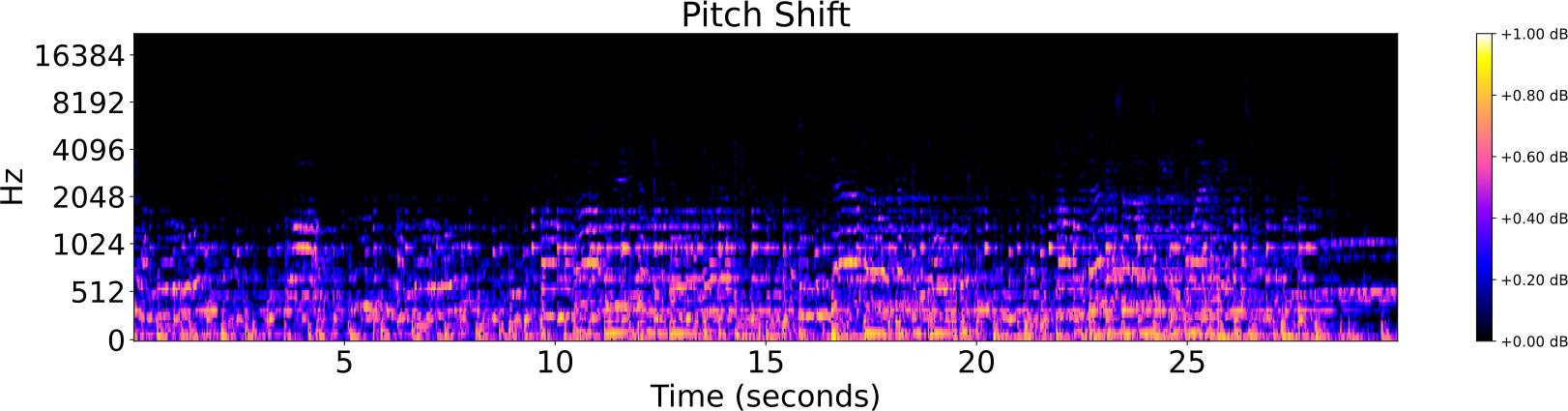
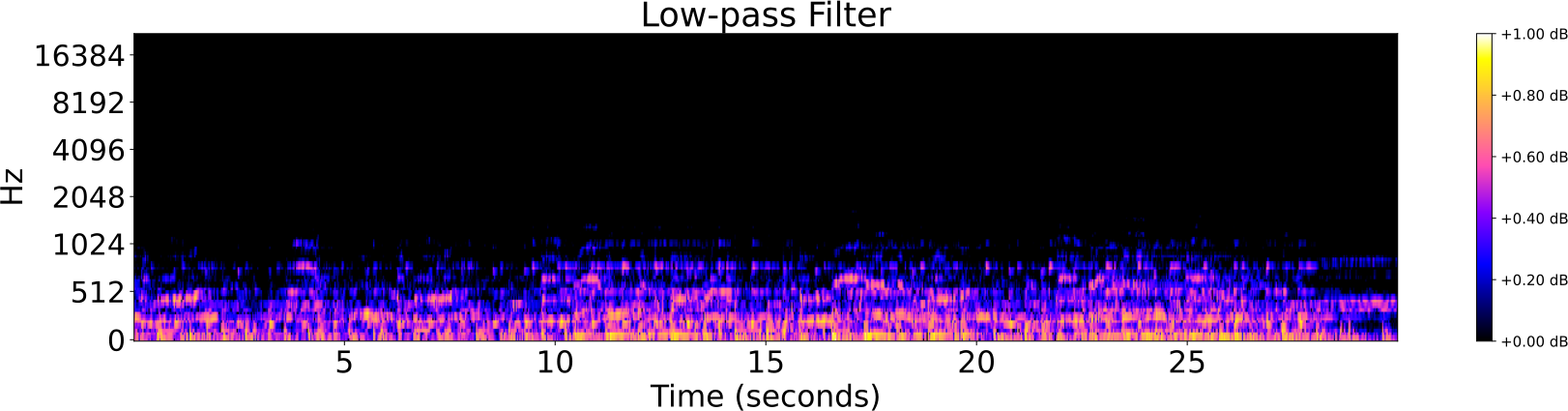

Audio Identification
Case study:
![]() Shazam
Shazam
- The algorithm has good performance for rigid obfuscations of audio tracks, such as:
- addition of noise,
- highpass/lowpass filter,
- reverberation.
-
The algorithm has poor performance for topological obfuscations of audio tracks, such as:
- change of pitch,
- change of tempo,
- mixed distortions; e.g. Music Obfuscator by Ben Grosser (2015).
Topological
Audio Identification
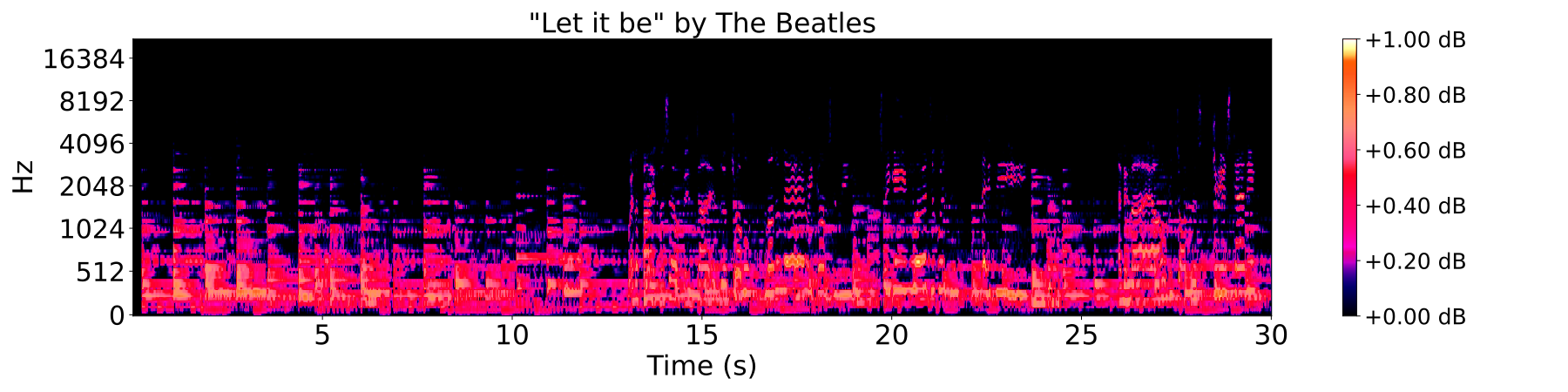
Topology of spectrograms
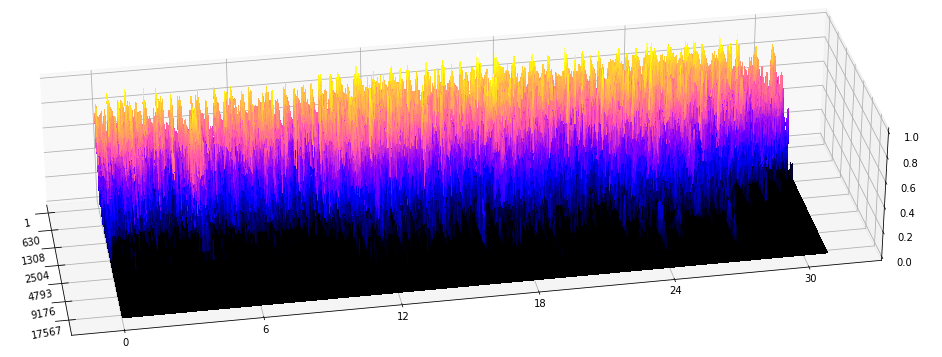
Topology of spectrograms
Mel-spectrograms as filtered cubical complexes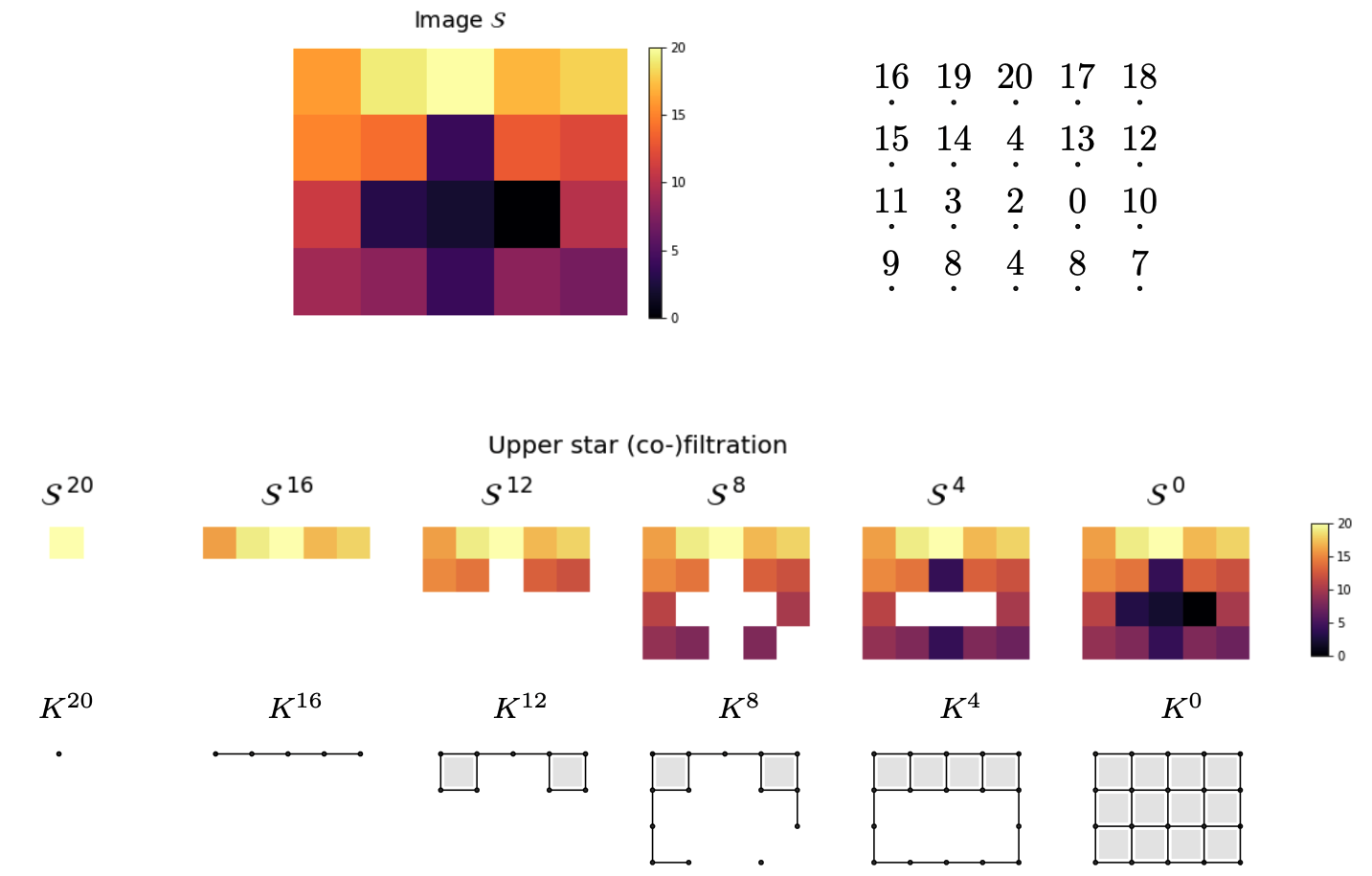
Topology of spectrograms
Mel-spectrograms as filtered cubical complexes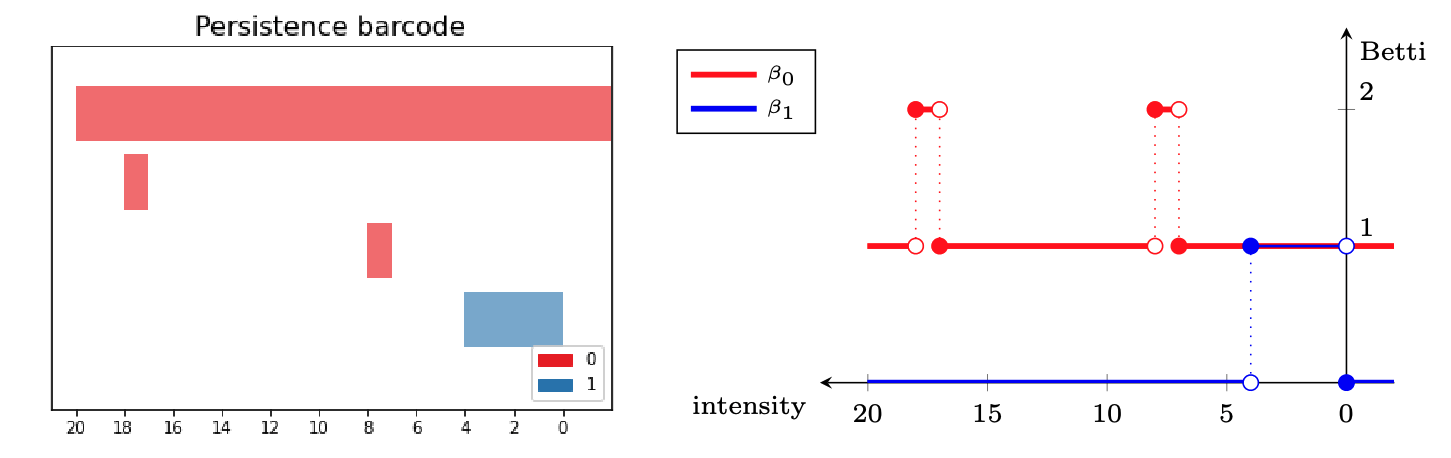
Topology of spectrograms
Topology of spectrograms
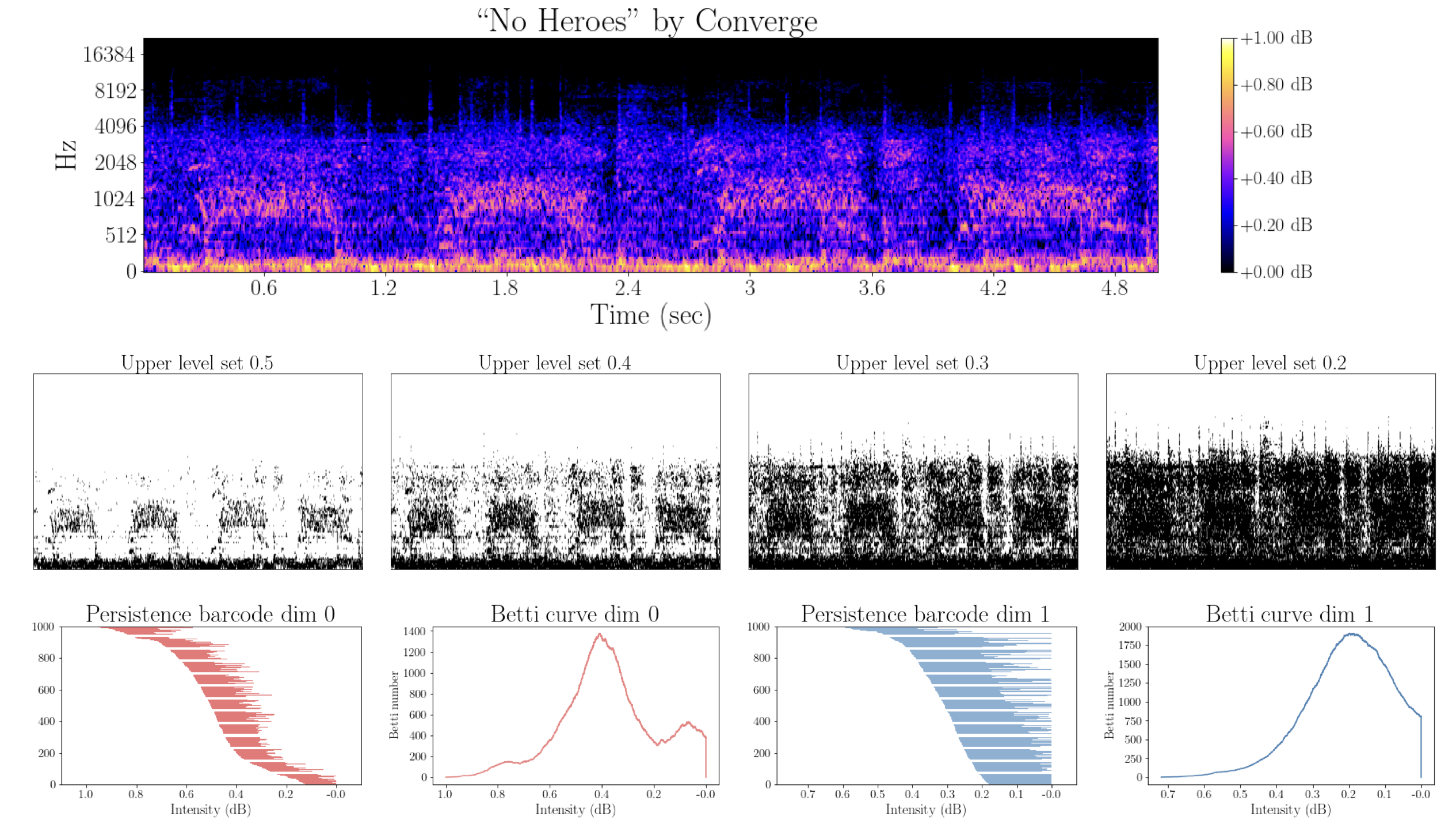
Topology of spectrograms

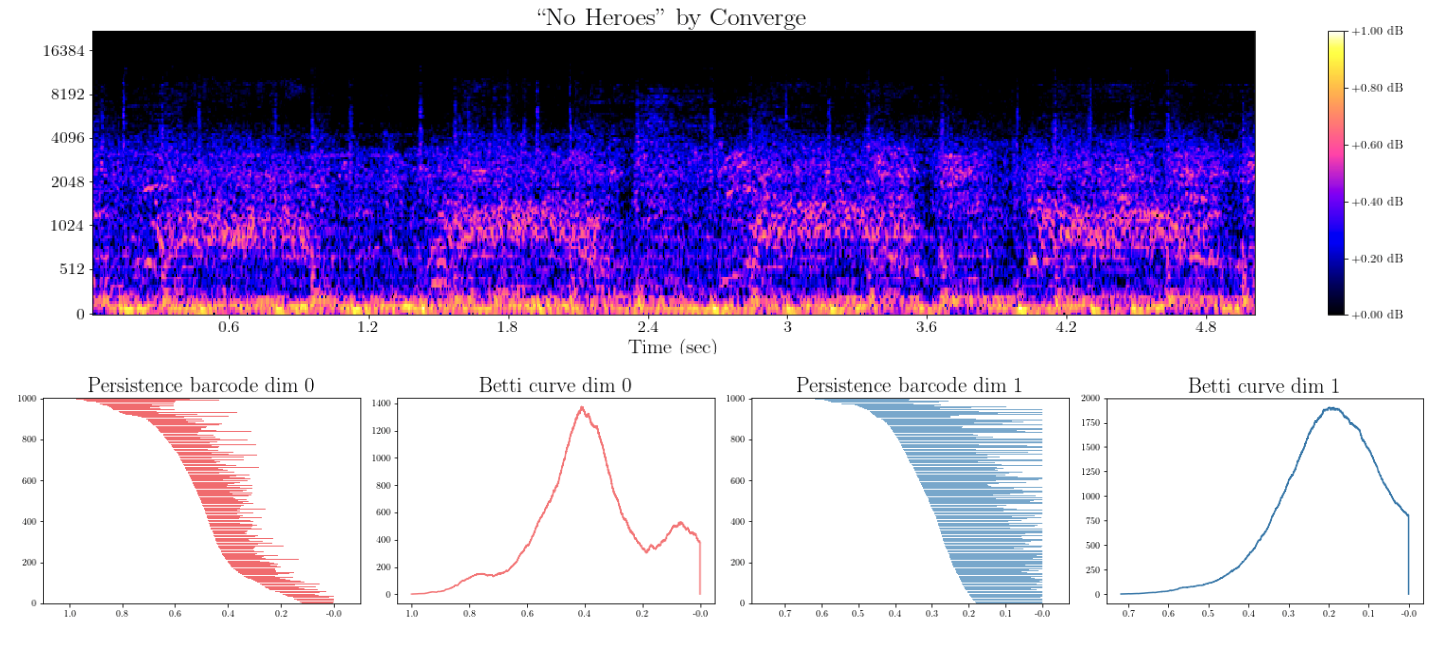
Topology of spectrograms

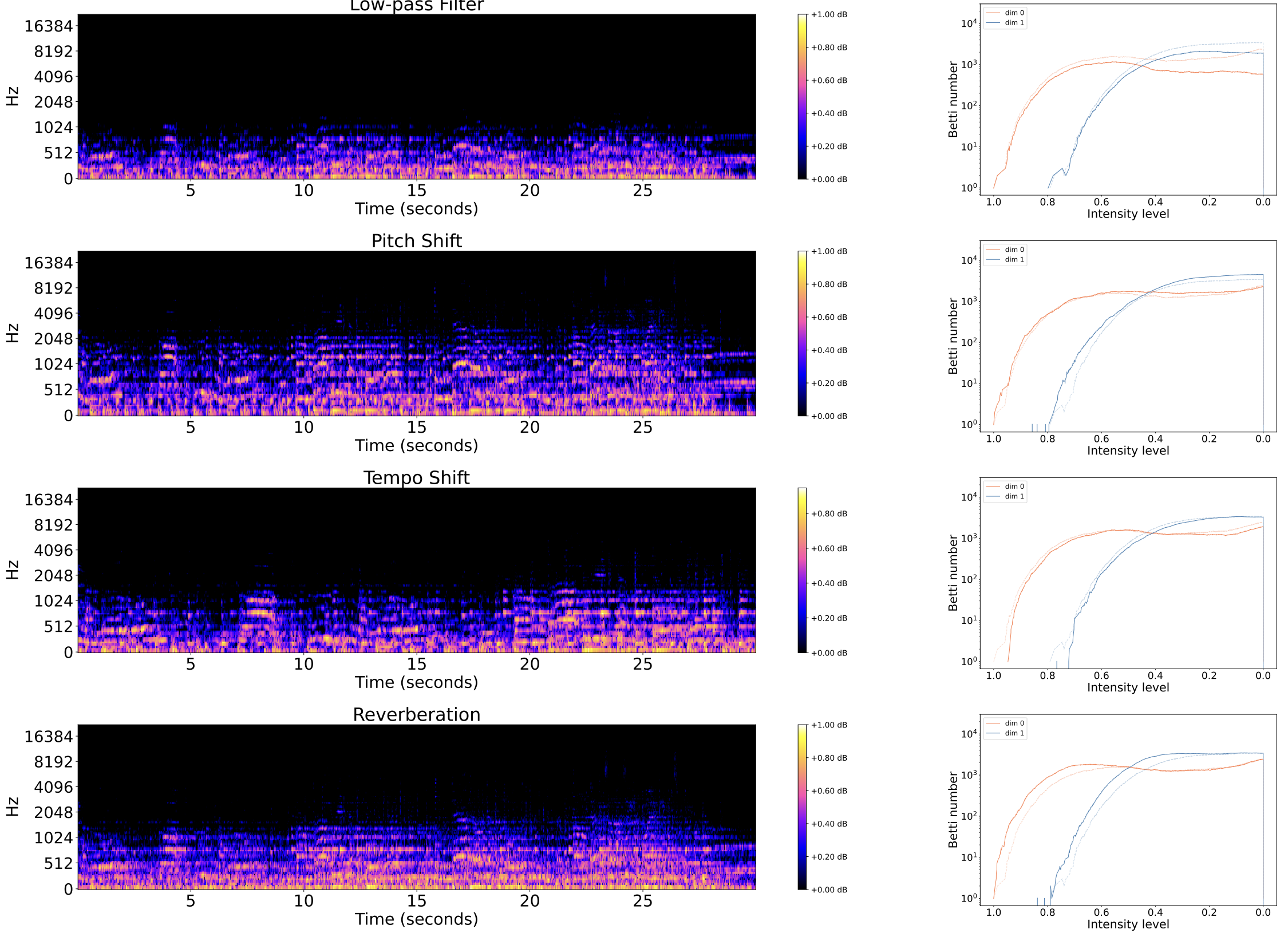
Topological fingerprints
Topological fingerprints
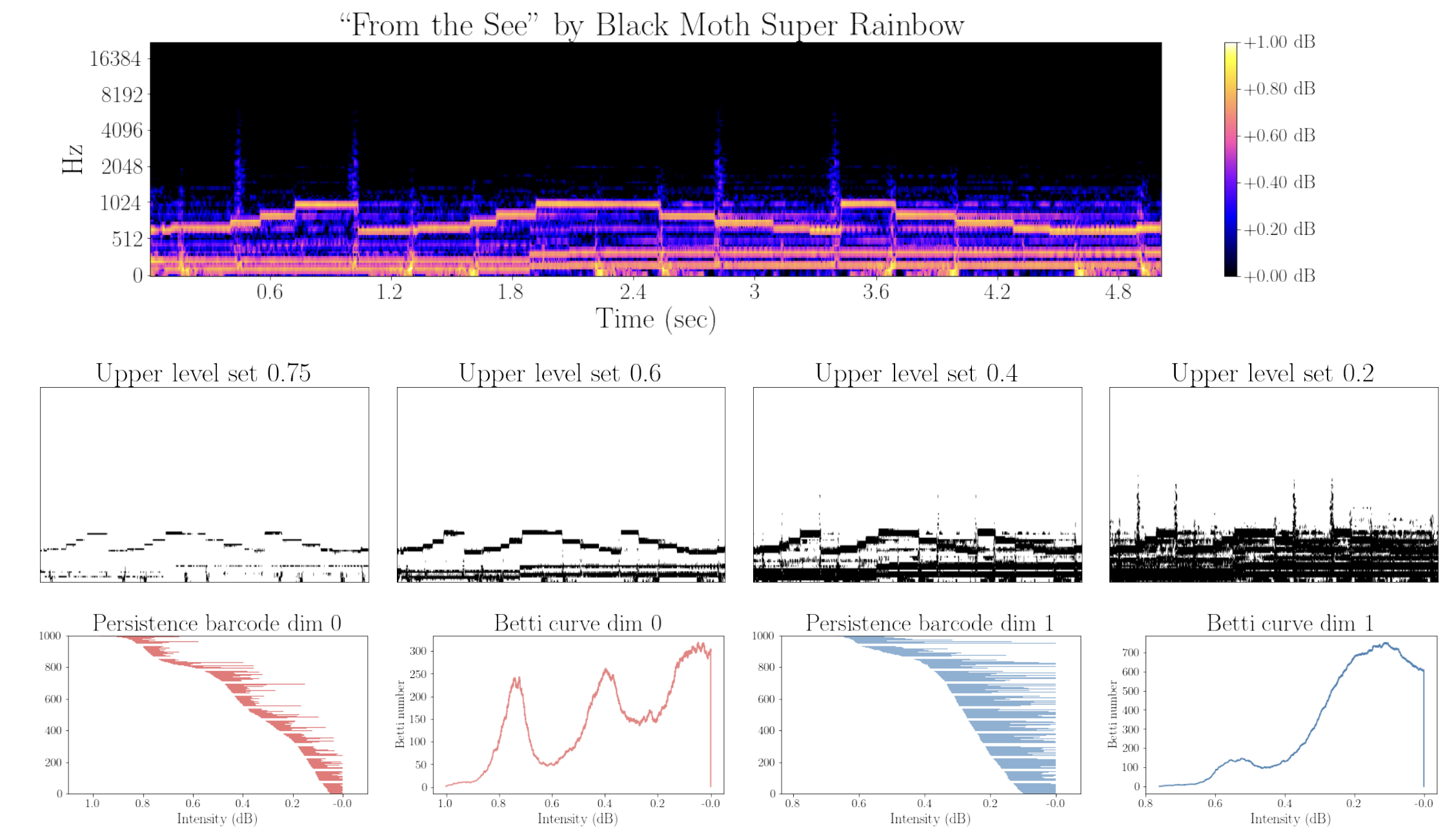
Let $\mathcal S$ denote the mel-spectrogram of an audio track $s:[0,T]\to \mathbb{R}$.
- Local spectral decompositions: Given $\omega$ a window size and $0<\tau<1$ an overlap constant, we subdivide $\mathcal S$ into a set of $\tau$-overlapping windows $W_0, W_1, \dots, W_k$ of $\omega$ seconds duration. We normalize the range of every window as $\frac{W_i-\min(W_i)}{\max(W_i)-\min(W_i)}.$ Let $t_i$ be the mid-time point of $W_i$.




Topological fingerprints
Let $\mathcal S$ denote the mel-spectrogram of an audio track $s:[0,T]\to \mathbb{R}$.
- Local persistence signatures: For each (normalized) window $W_i$, we compute the persistent homology of the associated upper-filtered cubical complex for dimensions 0 and 1.
We encode the persistent barcodes as a family of Betti curves $\{\beta_{i,0}\}_{i=0}^{k}$ and $\{\beta_{i,1}\}_{i=0}^{k}$ for dimensions 0 and 1, respectively.
Topological fingerprints
Let $\mathcal S$ denote the mel-spectrogram of an audio track $s:[0,T]\to \mathbb{R}$.
- Fingerprint: The topological fingerprint of the audio track $s$ with the resolution given by the parameters $\omega$ and $\tau$ is defined as the set of triples ${(t_i, \beta_{i,0}, \beta_{i,1})}_{i=0}^{k}$.
$~~~~~~~~~~~~t_0~~~~~~~~~~~~~~~~~~~~~~~t_1~~~~~~~~~~~~~~~~~~~~t_2~~~~~~~~~~~~~~~~~~~~~t_3~~~~~~~~~~~~~~~~~~~~~~t_4~~~~~~~~~~~~~~~~~~~~~t_5 \dots$
Comparing fingerprints
Comparing fingerprints
- Distance: Let $s$, $s'$ be two audio tracks and let ${(t_i, \beta_{i,0}, \beta_{i,1})}_{i=0}^{k}, {(t_j', \beta'_{j,0}, \beta'_{j,1})}_{j=0}^{k'}$ be its associated fingerprints.


$~~~~$
$~~~~~~~~~~~~~~~~t_0~~~~~~~~~~~~~~~~t_1~~~~~~~~~~~~~~~~t_2~~~~~~~~~~~~~~~t_3~~~~~~~~~~~~~~~t_4~~\dots~~~~~~~~~~~~~~~~~~t'_0~~~~~~~~~~~~~~~~t'_1~~~~~~~~~~~~~~~~t'_2~~~~~~~~~~~~~~~~t'_3~~~~~~~~~~~~~~~t'_4~~\dots$
Comparing fingerprints
- Distance: Let $s$, $s'$ be two audio tracks and let ${(t_i, \beta_{i,0}, \beta_{i,1})}_{i=0}^{k}, {(t_j', \beta'_{j,0}, \beta'_{j,1})}_{j=0}^{k'}$ be its associated fingerprints.
For every homological dimension $d=0,1$, the $d$-Betti distance matrix $M_d$ between $s$ and $s'$ is defined as \[ (M_d)_{i,j} = \Vert \beta_{i,d} - \beta'_{j,d} \Vert_{L^1}. \]
We summarize the distance between every pair of windows $W_i$ and $W_j'$ as \[ C_{i,j} = \lambda (M_0)_{i,j} + (1-\lambda) (M_1)_{i,j} \] for a parameter $0\leq \lambda\leq 1$.
Comparing fingerprints
- Matching: We compare $s$ and $s'$ via a minimum-cost matching in $C$.
Comparing fingerprints
- Matching: We compare $s$ and $s'$ via a minimum-cost matching in $C$.
Comparing fingerprints
- Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.
Comparing fingerprints
- Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.
For $m\geq 1$, compute $\bar t'_{j_i} = \mathrm{median} \{t_{j_{i-m}},\dots, t_{j_{i-1}}, t_{j_i}, t_{j_{i+1}}, \dots, t_{j_{i+m}}\}$, the moving median at $t_{j_i}$. Consider $\bar P=\{( t_{i}, \bar t_{j_i}'): i =1,\dots,k\}$.
Comparing fingerprints
- Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.
For $m\geq 1$, compute $\bar t'_{j_i} = \mathrm{median} \{t_{j_{i-m}}, t_{j_{i-m+1}}, \dots, t_{j_{i-1}}, t_{j_i}\}$, the moving median at $t_{j_i}$. Consider $\bar P=\{( t_{i}, \bar t_{j_i}'): i =1,\dots,k\}$.
We assess the functional increasing dependency of the points in $P$ as \[ \rho_{\bar P} = \mathrm{Pearson}\{(t_i), (\bar{t}'_{j_i})\}. \]
Comparing fingerprints
- Scoring: We quantify the degree of temporal-order preservation in the matching as follows. Suppose $k < k'$. Let $P = \{(t_{1}, t'_{j_1}), \dots, (t_{i}, t'_{j_k})\}$ be the set of mid-points of matched windows, with $t_1< t_2< \dots< t_k$.
For $m\geq 1$, compute $\bar t'_{j_i} = \mathrm{median} \{t_{j_{i-m}}, t_{j_{i-m+1}}, \dots, t_{j_{i-1}}, t_{j_i}\}$, the moving median at $t_{j_i}$. Consider $\bar P=\{( t_{i}, \bar t_{j_i}'): i =1,\dots,k\}$.
We assess the functional increasing dependency of the points in $P$ as \[ \rho_{\bar P} = \mathrm{Pearson}\{(t_i), (\bar{t}'_{j_i})\}. \]
Experimental Results
Experimental Results
Music Obfuscator by Ben Grosser
| Song | Shazam (60 sec) |
|---|---|
| Smells Like Teen Spirit | No |
| Get Lucky | No |
| Giant Steps | No |
| Stairway to Heaven | Yes |
| Headlines | Yes |
| Blue in Green | No |
| You’re Gonna Leave | No |
| Blue Ocean Floor | No |
Experimental Results
Music Obfuscator by Ben Grosser
| Song | Shazam (60 sec) | Correlation (60-30 sec) |
|---|---|---|
| Smells Like Teen Spirit | No | 0.83208 |
| Get Lucky | No | 0.99906 |
| Giant Steps | No | 0.83904 |
| Stairway to Heaven | Yes | 0.88533 |
| Headlines | Yes | 0.91173 |
| Blue in Green | No | 0.89276 |
| You’re Gonna Leave | No | 0.71766 |
| Blue Ocean Floor | Yes | 0.51332 |
Experimental Results
Spotify Database + PySOX Transformer
-
 Spotify Web API. Dataset of 30 seconds preview snippets of (~135.000) songs.
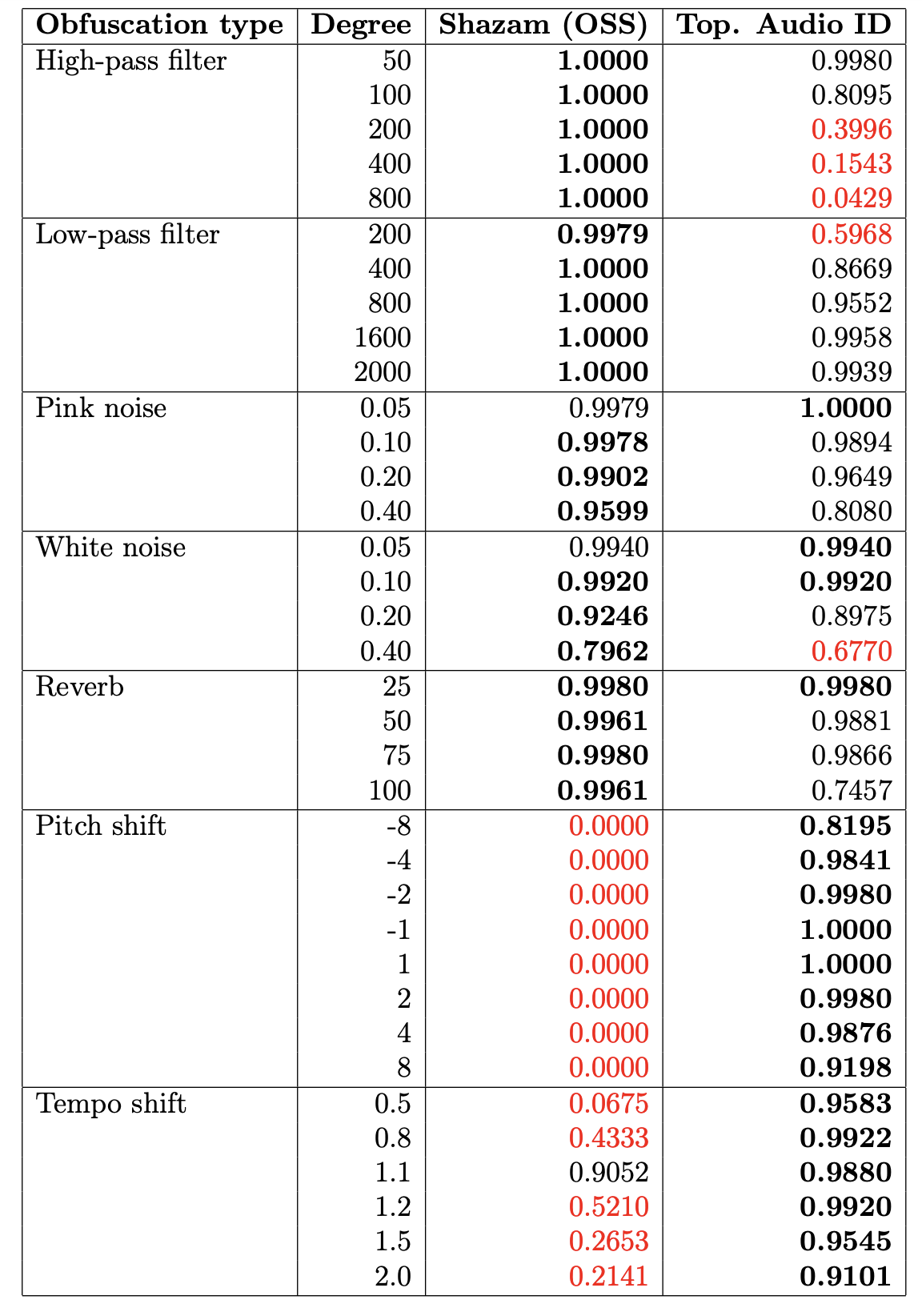
Spotify Web API. Dataset of 30 seconds preview snippets of (~135.000) songs. - PySOX Transformer. Every audio track has been then manipulated according to seven types of obfuscations in a range of different degrees of magnitude.
- Positive and negative pairs. For every obfuscation type and degree, we generated a random set of 1000 positive pairs (36000 in total). We also generated a random set of 36000 negative pairs.
| Obfuscation type | Degree |
|---|---|
| Low Pass Filter | 200, 400, 800, 1600, 2000 |
| High Pass Filter | 50, 100, 200, 400, 800, 1200 |
| White Noise | 0.05, 0.10, 1.20, 0.40 |
| Pink Noise | 0.05, 0.10, 1.20, 0.40 |
| Reverberation | 25, 50, 75, 100 |
| Tempo | 0.50, 0.80, 1.1 1.2, 1.50, 2.00 |
| Pitch | -8, -4, -2, -1, 1, 2, 4, 8 |
Experimental Results
Future work
the 1 vs N problem
Given an audio track $s$ and a database $\mathcal D$, identify an element $s'\in \mathcal D$ with the same audio content as $s$.
Future work
the 1 vs N problem
Given an audio track $s$ and a database $\mathcal D$, identify an element $s'\in \mathcal D$ with the same audio content as $s$.
- The search algorithm involves the comparison of the sample fingerprint with the (already computed) database fingerprints.
Future work
the 1 vs N problem
Given an audio track $s$ and a database $\mathcal D$, identify an element $s'\in \mathcal D$ with the same audio content as $s$.
- The search algorithm involves the comparison of the sample fingerprint with the (already computed) database fingerprints.
-
Some ideas to generalize the 1 vs 1 algorithm to the 1 vs N problem:
- Clustering of the database by content.
- Subdivide every audio track from the database in blocks of $T$ seconds (e.g. 60 sec).
References
-
W. Reise, X. Fernandez, M. Dominguez, H.A. Harrington, M. Beguerisse-Diaz. Topological fingerprints for audio identification (2023) SIAM Journal of Data Science (accepted) arXiv:2309.03516

