
Computational topology for data analysis
XIMENA FERNANDEZ


TOPOLOGICAL DATA ANALYSIS
Topological Data Analysis
DATA$\mathbb{X}_n \subset \mathbb{R}^D$

Topological Data Analysis
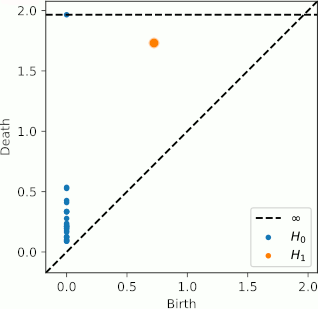
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Inference problem: How to estimate topological properties of $X$ from $\mathbb{X}_n$?
$\mathbb{X}_n \subset \mathbb{R}^D$

$X$

Topological Data Analysis
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Inference problem: How to estimate topological properties of $X$ from $\mathbb{X}_n$?
$\mathbb{X}_n \subset \mathbb{R}^D$

Topological Data Analysis
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Inference problem: How to estimate topological properties of $X$ from $\mathbb{X}_n$?
$\mathbb{X}_n \subset \mathbb{R}^D$

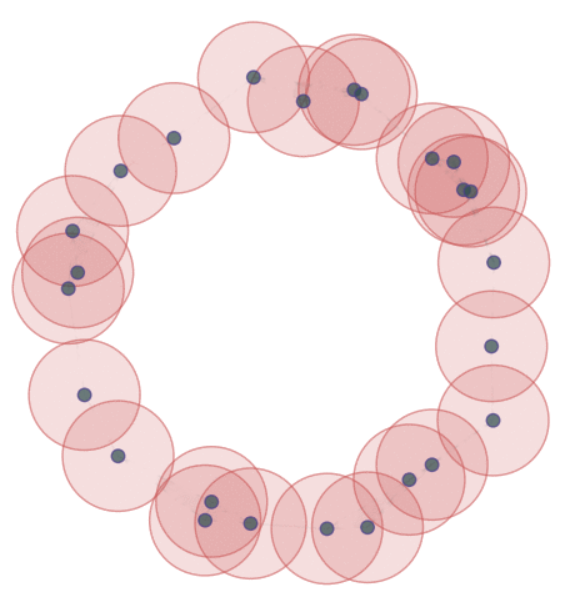
$\text{Evolving thickenings}$

Topological Data Analysis
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Inference problem: How to estimate topological properties of $X$ from $\mathbb{X}_n$?
$\mathbb{X}_n \subset \mathbb{R}^D$

$\text{Evolving thickenings}$

$\text{Sequence of combinatorial spaces}$
 $\epsilon = 0 ~~~~~~~\epsilon = 0.7 ~~~~~~~\epsilon = 1 ~~~~~~~\epsilon = 2$
$\epsilon = 0 ~~~~~~~\epsilon = 0.7 ~~~~~~~\epsilon = 1 ~~~~~~~\epsilon = 2$
Topological Data Analysis
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Inference problem: How to estimate topological properties of $X$ from $\mathbb{X}_n$?
$\mathbb{X}_n \subset \mathbb{R}^D$

$\text{Sequence of combinatorial spaces}$

$\text{Persistent Homology}$

Persistent homology
Input dataset $X$.
- Combinatorics: construct an increasing family $\{X_\epsilon\}$ of complexes around $X$, where the indexing $\epsilon$ is a scale parameter in $\mathbb R\geq 0$.
- Algebraic topology: compute the $d$-th homology vector spaces $H_d(X_\epsilon)$ for scales $\epsilon\in R_{\geq 0}$ and dimensions $d \in Z_{\geq 0}$.
- Representation theory: decompose each family of vector spaces $\{H_d(X_\epsilon)\colon \epsilon \geq 0\}$ into irreducible summands, thus producing a barcode.

Source: B. Rieck
Persistent homology
Input dataset $X$.
- Combinatorics: construct an increasing family $\{X_\epsilon\}$ of complexes around $X$, where the indexing $\epsilon$ is a scale parameter in $\mathbb R\geq 0$.
- Algebraic topology: compute the $d$-th homology vector spaces $H_d(X_\epsilon)$ for scales $\epsilon\in R_{\geq 0}$ and dimensions $d \in Z_{\geq 0}$.
- Representation theory: decompose each family of vector spaces $\{H_d(X_\epsilon)\colon \epsilon \geq 0\}$ into irreducible summands, thus producing a barcode.


Source: B. Rieck
Persistent homology
Input dataset $X$.
- Metric geometry: Stability property. Let $(X, d_X)$, $(Y, d_Y)$ be metric spaces. Then, \[d_B(\mathrm{dgm}(X, d_X), \mathrm{dgm}(Y, d_Y)) \leq d_{GH}((X, d_X),(Y, d_Y))\]
Source: B. Rieck
Persistent homology
Input dataset $X$.
- Metric geometry: Stability property. Let $(X, d_X)$, $(Y, d_Y)$ be metric spaces. Then, \[d_B(\mathrm{dgm}(X, d_X), \mathrm{dgm}(Y, d_Y)) \leq d_{GH}((X, d_X),(Y, d_Y))\]


Source: B. Rieck
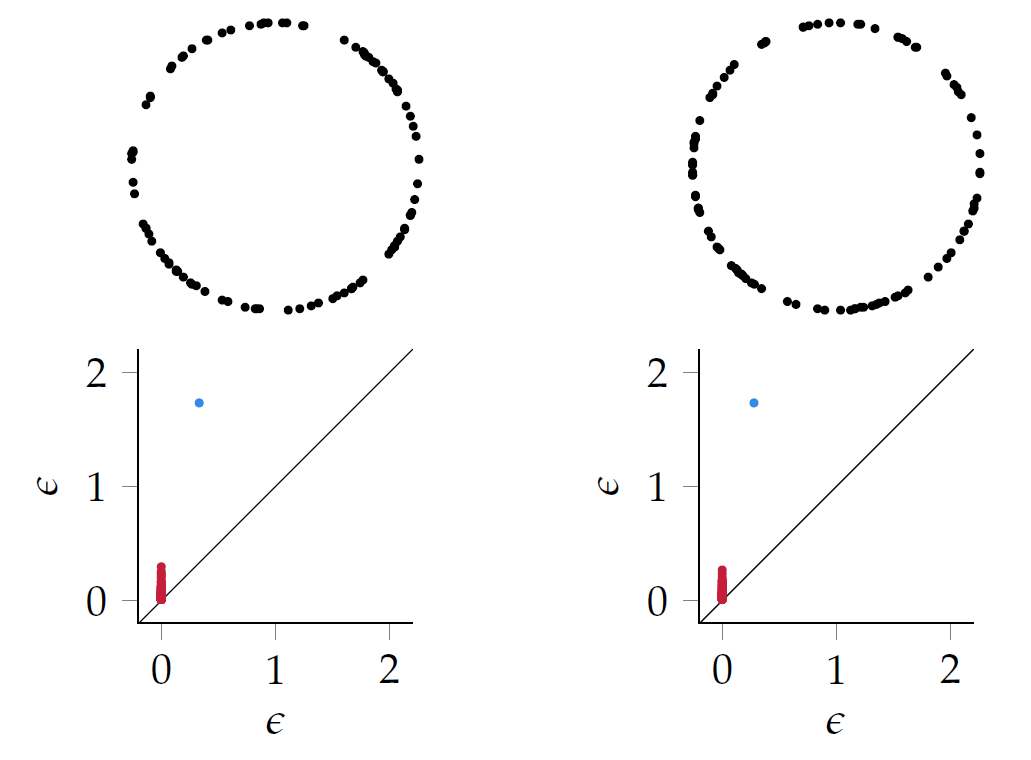
Persistent homology
Problem: Persistent homology is not robust in general to noise and outliers, and it might be very sensitive to the embedding in the ambient space.

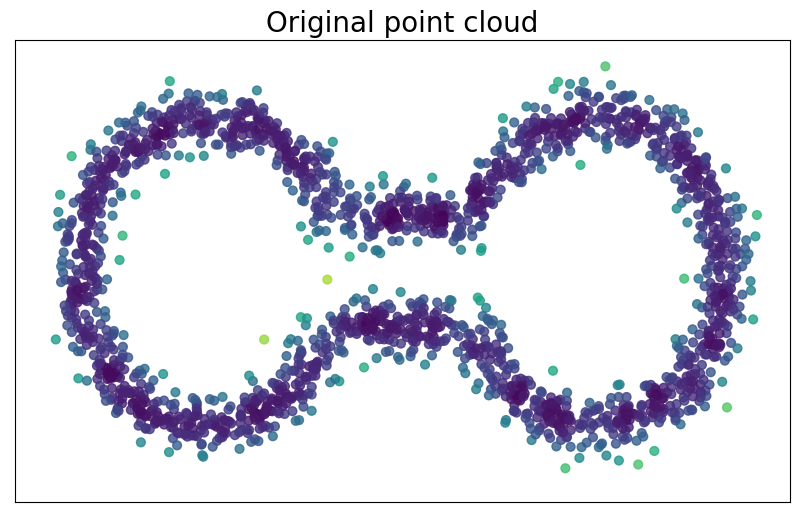
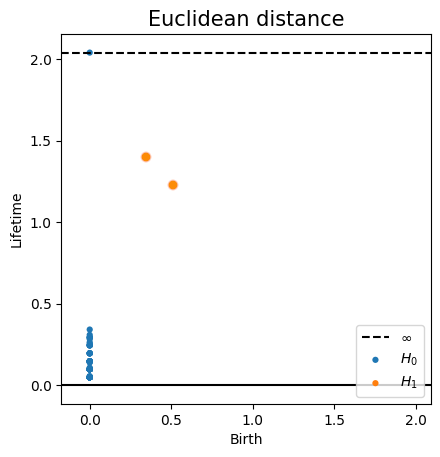
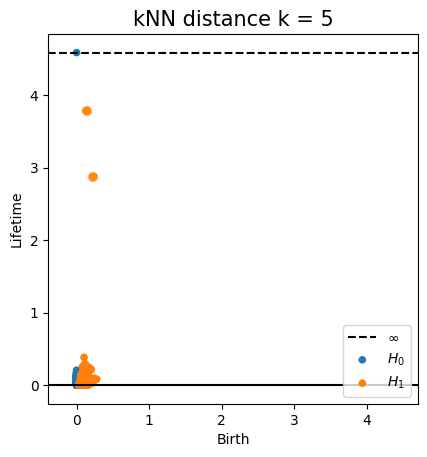
Data with density

Data with density
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ data points.
Assume that:
- $\mathbb{X}_n$ is a sample of a compact Riemannian manifold $\mathcal M$ of dimension $d$.
- The points are sampled according to a density $f\colon \mathcal M\to \mathbb R$.
Goal: Infer $'H_\bullet(\mathcal M, f)'$


X. Fernandez, E. Borghini, G. Mindlin, P. Groisman. 'Intrinsic persistent-homology via density-based metric learning'. Journal of Machine Learning Research. 24 (2023) 1-42.
Density-based geometry



Fermat principle
The path taken by a ray between two given points is the path that can be traversed in the least time.
That is, it is the extreme of the functional \[ \gamma\mapsto \int_{0}^1\eta(\gamma_t)||\dot{\gamma}_t|| dt \] with $\eta$ is the refraction index.

Density-based geometry
UNDERLYING SPACE
$\mathcal M \subseteq \mathbb{R}^D$ manifold, $f:\mathcal{M}\to \mathbb{R}_{>0}$ density.
For $q>0$, deformed Riemannian distance in $\mathcal{M}$ \[ d_{f,q}(x,y) = \inf_{\gamma:x\sim y} \int_{\gamma}\frac{1}{f(\gamma_t)^{q}}||\dot \gamma_t||dt. \]
Density-based geometry
UNDERLYING SPACE
$\mathcal M \subseteq \mathbb{R}^D$ manifold, $f:\mathcal{M}\to \mathbb{R}_{>0}$ density.
For $q>0$, deformed Riemannian distance in $\mathcal{M}$ \[ d_{f,q}(x,y) = \inf_{\gamma:x\sim y} \int_{\gamma}\frac{1}{f(\gamma_t)^{q}}||\dot \gamma_t||dt. \]

DATA
$\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ sample.
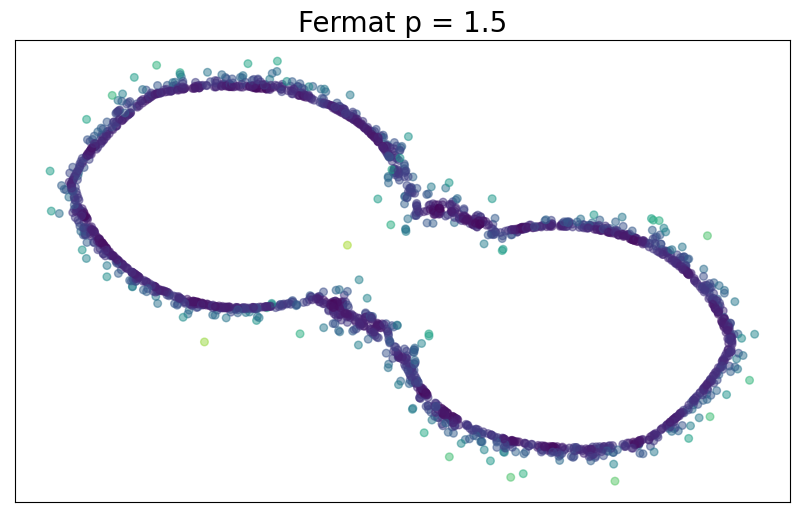
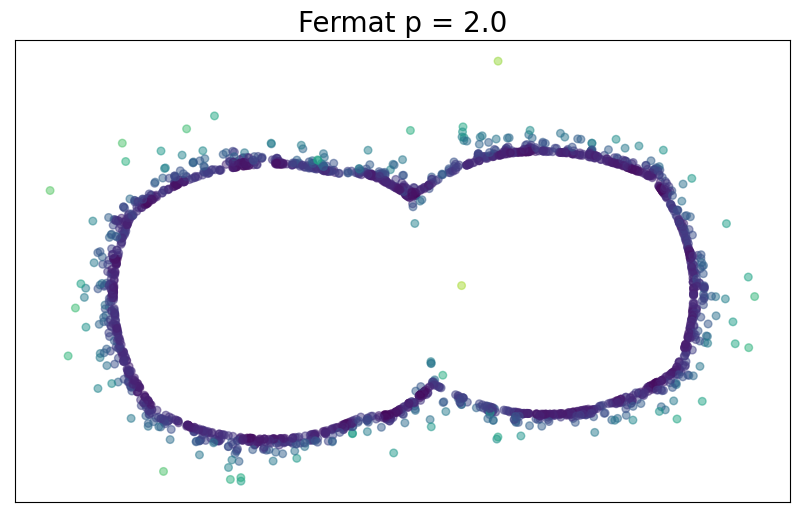
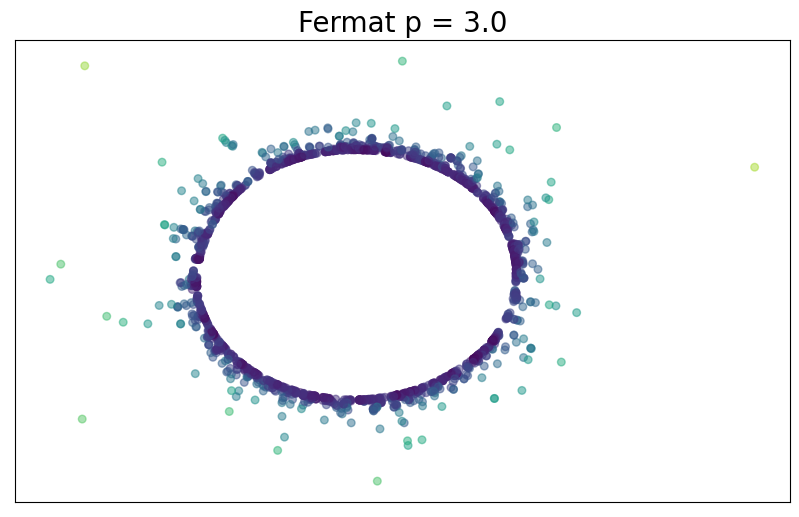
For $p> 1$, Fermat distance in $\mathbb{X}_n$ \[ d_{\mathbb{X}_n, p}(x,y) = \inf_{\gamma:x\sim y} \sum_{i=0}^{r}|x_{i+1}-x_i|^{p}. \]

Density-based geometry
Theorem (F., Borghini, Mindlin, Groisman)
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]


Density-based geometry
Theorem (F., Borghini, Mindlin, Groisman)
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]


Let $\mathcal{M}$ be a closed smooth $d$-dimensional Riemannian manifold embedded in $\mathbb{R}^D$. Let $\mathbb X_n\subseteq \mathcal{M}$ be a set of $n$ independent sample points with common smooth density $f:\mathcal{M}\to \mathbb{R}_{>0}$.
Given $p>1$ and $q=(p-1)/d$, there exists a constant $\mu = \mu(p,d)$ such that for every $\lambda \in \big((p-1)/pd, 1/d\big)$ and $\varepsilon>0$ there exist $\theta>0$ satisfying \[ \mathbb{P}\left( d_{GH}\left(\big(\mathcal{M}, d_{f,q}\big), \big(\mathbb{X}_n, {\scriptstyle \frac{n^{q}}{\mu}} d_{\mathbb{X}_n, p}\big)\right) > \varepsilon \right) \leq \exp{\left(-\theta n^{(1 - \lambda d) /(d+2p)}\right)} \] for $n$ large enough.
$~$Density-based geometry
Theorem (F., Borghini, Mindlin, Groisman)
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]


Density-based Persistent Homology
Theorem (F., Borghini, Mindlin, Groisman)
\[\mathrm{dgm}\Big(\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\Big)\xrightarrow[n\to \infty]{B}\mathrm{dgm}\Big(\big(\mathcal{M}, d_{f,q}\big)\Big) ~~~ \text{ for } q = (p-1)/d\]


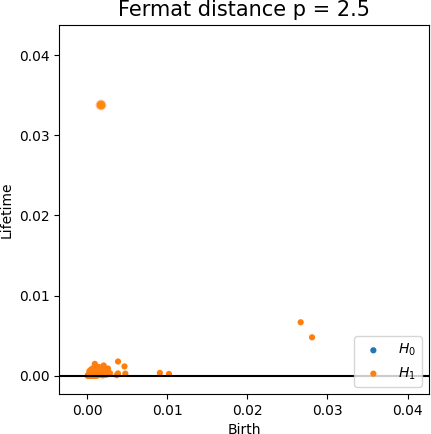
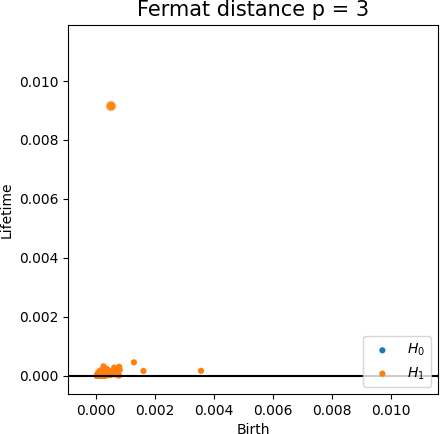
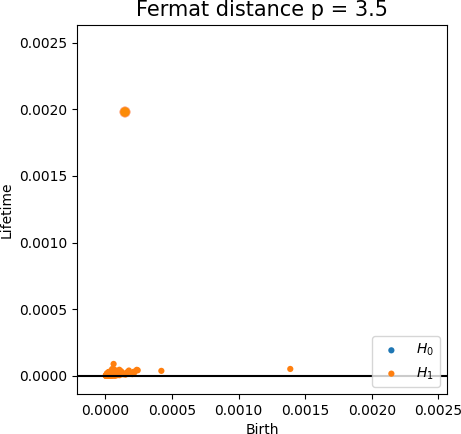
Density-based Persistent Homology
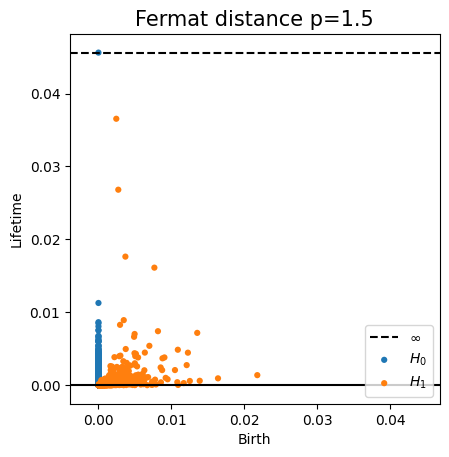
Robustness to outliers
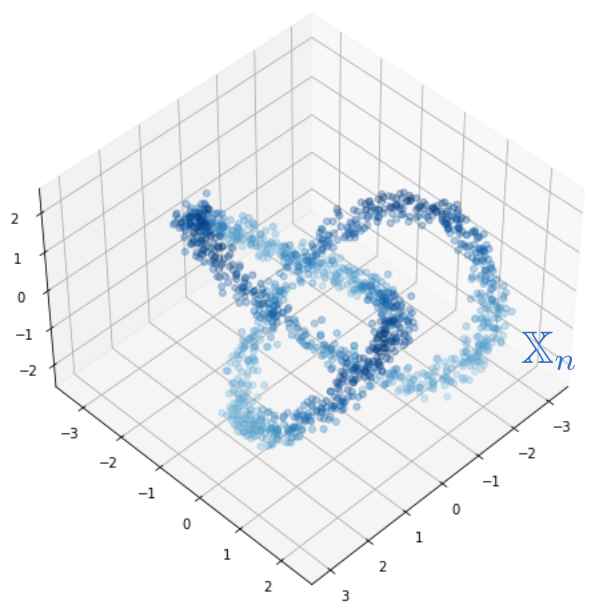
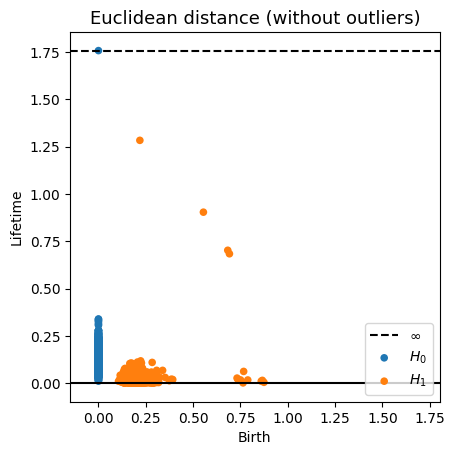
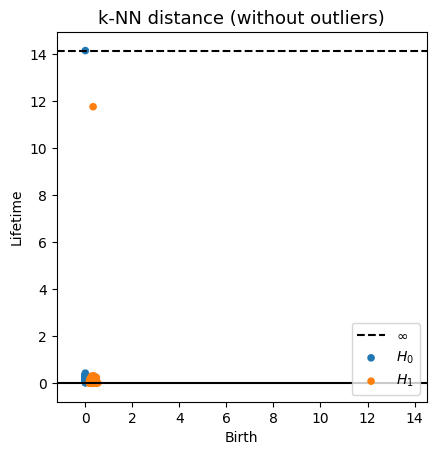
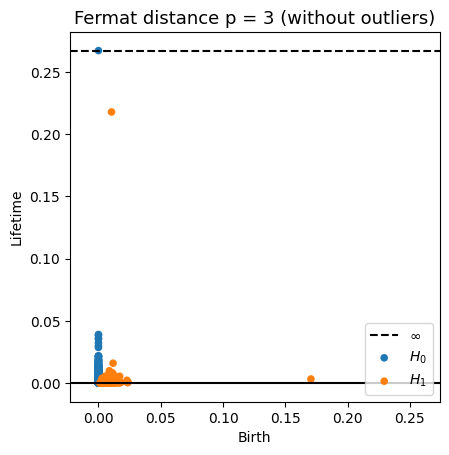
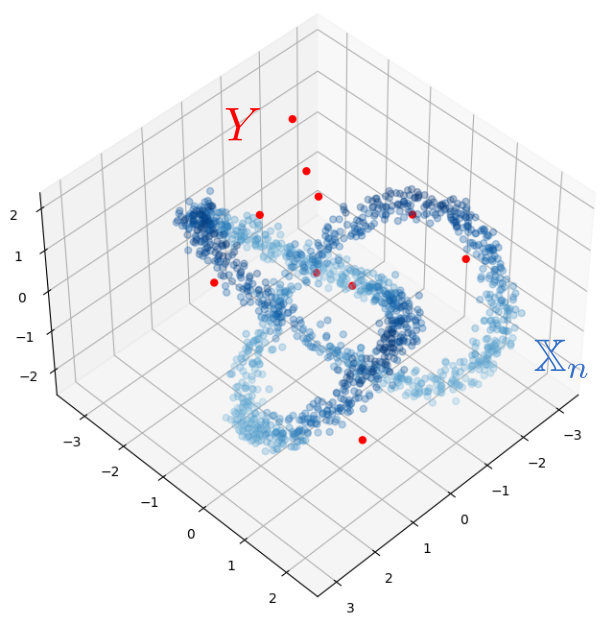
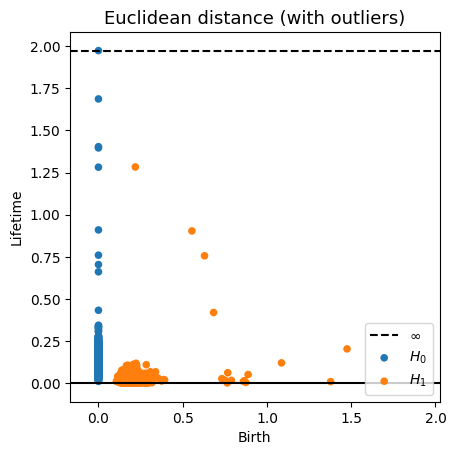
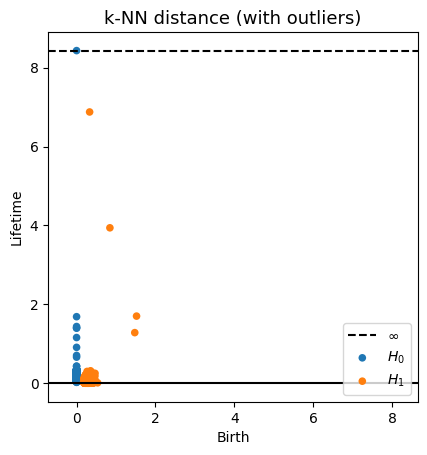
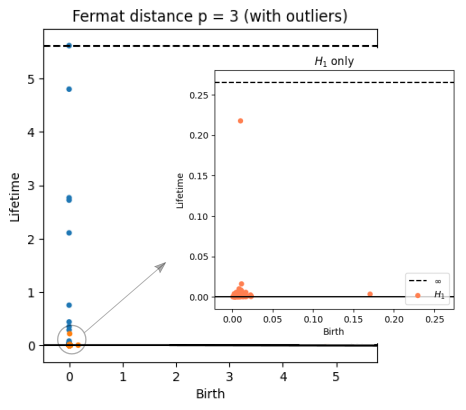
Density-based Persistent Homology
Robustness to outliers
Prop (F., Borghini, Mindlin, Groisman, 2023)
Let $\mathbb{X}_n$ be a sample of $\mathcal{M}$ and let $Y\subseteq \mathbb{R}^D\smallsetminus \mathcal{M}$ be a finite set of outliers. Let $\delta = \displaystyle \min\Big\{\min_{y\in Y} d_E(y, Y\smallsetminus \{y\}), ~d_E(\mathbb X_n, Y)\Big\}$.
Then, for all $k>0$ and $p>1$,
\[
\mathrm{dgm}_k(\mathrm{Rips}_{<\delta^p}(\mathbb{X}_n \cup Y, d_{\mathbb{X}_n\cup Y, p})) = \mathrm{dgm}_k(\mathrm{Rips}_{<\delta^p}(\mathbb{X}_n, d_{\mathbb{X}_n, p}))
\]
where $\mathrm{Rips}_{<\delta^p}$ stands for the Rips filtration up to parameter $\delta^{p}$ and $\mathrm{dgm}_k$ for the persistent homology of deg $k$.
 $~~~~~~~~~$
$~~~~~~~~~$
APPLICATIONS
1. Topological methods in time series Analysis
X. Fernandez, E. Borghini, G. Mindlin, P. Groisman. 'Intrinsic persistent-homology via density-based metric learning'. Journal of Machine Learning Research. 24 (2023) 1-42.
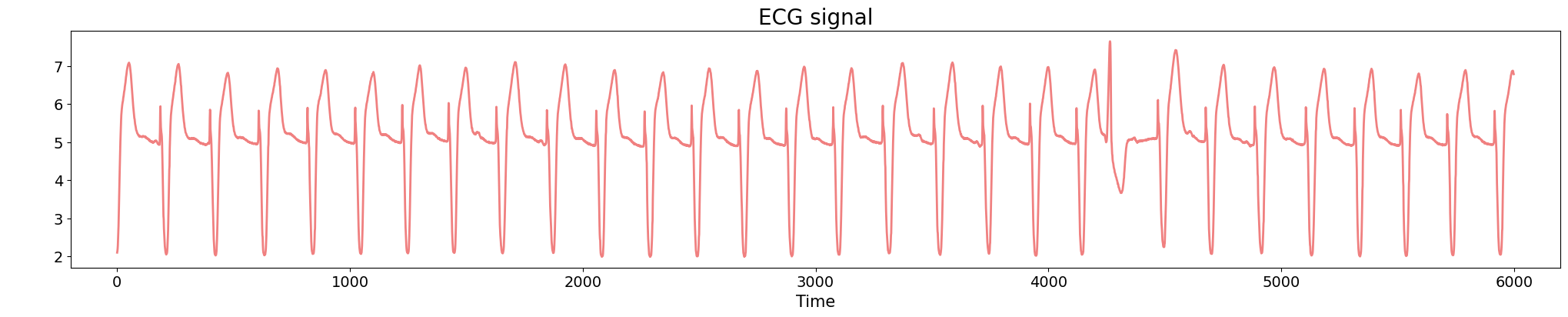
1. Topological methods in time series Analysis
Anomaly detection en ECG

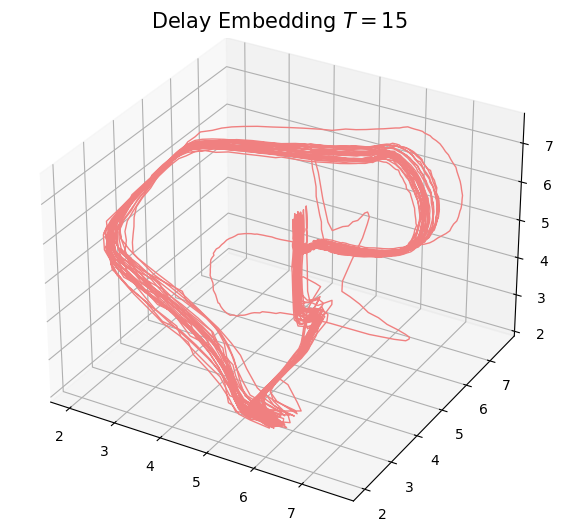
Delay embedding:
Given $T$ the time delay and $D$ the embedding dimension,
\[\{\big(\varphi(t), \varphi(t+T), \varphi(t+2 T) \dots, \varphi(t+(D-1)T)\big): t\in \mathbb R\}\subseteq \mathbb{R}^D\]
1. Topological methods in time series Analysis
Anomaly detection in ECG
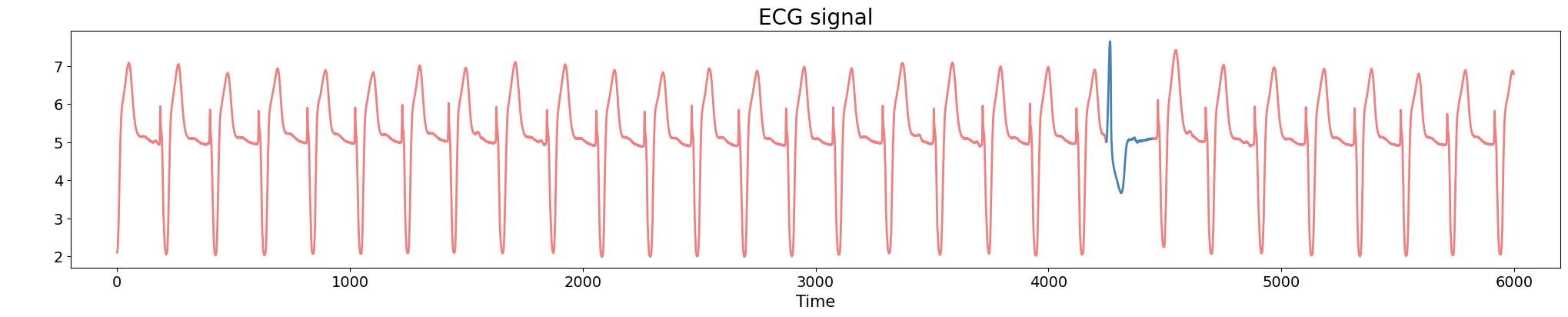
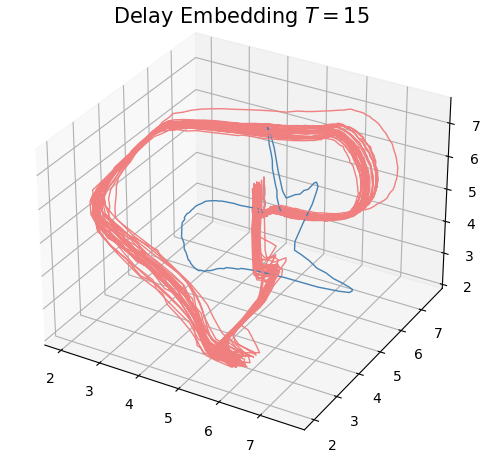
Delay embedding:
Given $T$ the time delay and $D$ the embedding dimension,
\[\{\big(\varphi(t), \varphi(t+T), \varphi(t+2 T) \dots, \varphi(t+(D-1)T)\big): t\in \mathbb R\}\subseteq \mathbb{R}^D\]
1. Topological methods in time series Analysis
Anomaly detection in ECG


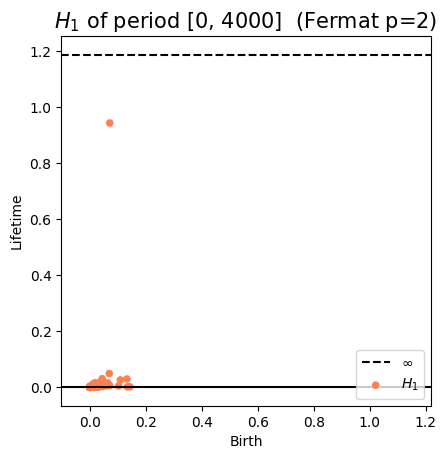
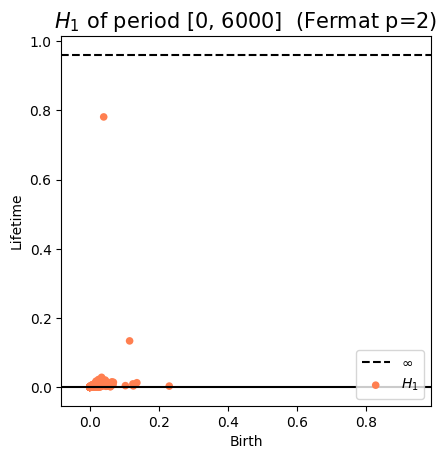
1. Topological methods in time series Analysis
Anomaly detection in ECG
 \[t\mapsto \mathrm{dgm}_t\]
Approximate Derivative: $\frac{d_B(\mathrm{dgm}_t, \mathrm{dgm}_{t'})}{|t'-t|}$
\[t\mapsto \mathrm{dgm}_t\]
Approximate Derivative: $\frac{d_B(\mathrm{dgm}_t, \mathrm{dgm}_{t'})}{|t'-t|}$

1. Topological methods in time series Analysis
Pattern detection in birdsongs

Source data: Private experiments. Laboratory of Dynamical Systems, University of Buenos Aires.
1. Topological methods in time series Analysis
Pattern detection in birdsongs

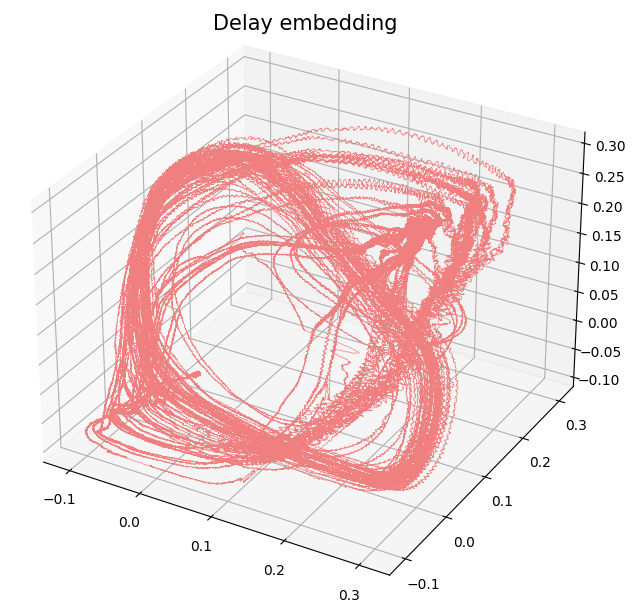
1. Topological methods in time series Analysis
Pattern detection in birdsongs


1. Topological methods in time series Analysis
Pattern detection in birdsongs

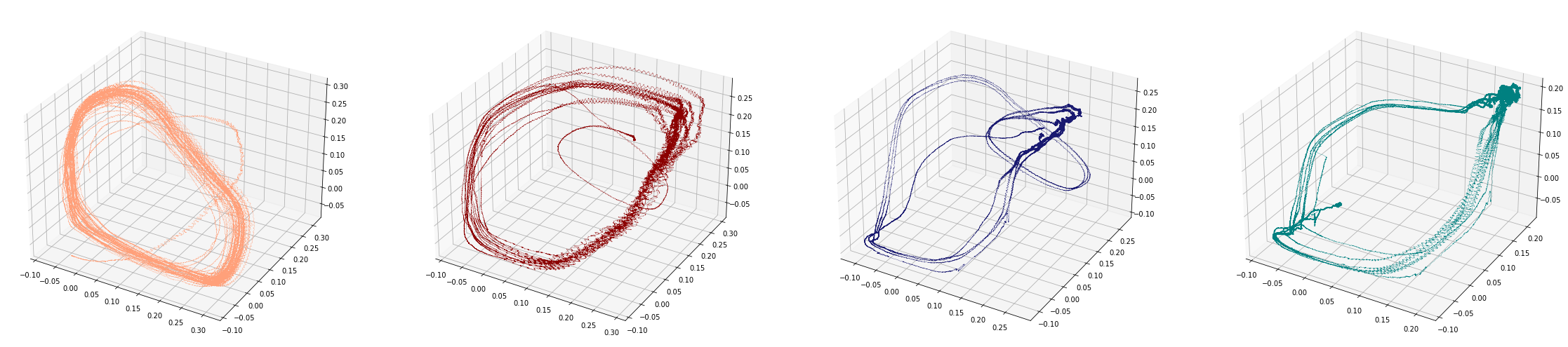

1. Topological methods in time series Analysis
Pattern detection in birdsongs
 \[t\mapsto \mathrm{dgm}_t\]
Approximate Derivative
\[t\mapsto \mathrm{dgm}_t\]
Approximate Derivative

2. Topological Methods in Biomedicine
Epileptic seizure detection
$~~~~~$X. Fernandez, D. Mateos. Topological biomarkers for real-time epileptic seizures. Preprint arXiv:2211.02523 (2024)
2. Topological Methods in Biomedicine
Epileptic seizure detection
Problem: Given a physiological recording of the brain activity, algorithmically detect in real time epileptic seizures.

$~~~~~$X. Fernandez, D. Mateos. Topological biomarkers for real-time epileptic seizures. Preprint arXiv:2211.02523 (2024)
2. Topological Methods in Biomedicine
Epileptic seizure detection
- Let $\varphi_1, \varphi_2, \dots \varphi_N:[0,T]\to \mathbb{R}$ a set of signals (EEG, MEG, etc.)
- Given a window size $W$, compute the sliding window embedding for every instant of time $t_0$ $$\big\{\big(\varphi_1(t), \varphi_2(t), \dots, \varphi_N(t)\big):t\in [t_0-W, t_0]\big\}\subseteq \mathbb{R}^N.$$
2. Topological Methods in Biomedicine
Epileptic seizure detection
- Let $\varphi_1, \varphi_2, \dots \varphi_N:[0,T]\to \mathbb{R}$ a set of signals (EEG, MEG, etc.)
- Given a window size $W$, compute the sliding window embedding $\Big\{\big(\varphi_1(t), \dots, \varphi_N(t)\big): t\in [t_0-W, t_0]\Big\}\subseteq \mathbb R^N$
- Compute the persistent homology of the time evolving point clouds.
2. Topological Methods in Biomedicine
Epileptic seizure detection
- Let $\varphi_1, \varphi_2, \dots \varphi_N:[0,T]\to \mathbb{R}$ a set of signals (EEG, MEG, etc.)
- Given a window size $W$, compute the sliding window embedding $\Big\{\big(\varphi_1(t), \dots, \varphi_N(t)\big):t\in [t_0-W, t_0]\Big\}\subseteq \mathbb R^N$
- Compute the persistent homology of the time evolving point clouds.
- Estimate the derivative of the path of persistence diagrams.

2. Topological Methods in Biomedicine
Epileptic seizure detection
- Let $\varphi_1, \varphi_2, \dots \varphi_N:[0,T]\to \mathbb{R}$ a set of signals (EEG, MEG, etc.)
- Given a window size $W$, compute the sliding window embedding $\Big\{\big(\varphi_1(t), \dots, \varphi_N(t)\big):t\in [t_0-W, t_0]\Big\}\subseteq \mathbb R^N$
- Compute the persistent homology of the time evolving point clouds.
- Estimate the derivative of the path of persistence diagrams.

2. Topological Methods in Biomedicine
Epileptic seizure detection
EEG (CH-MIT Database)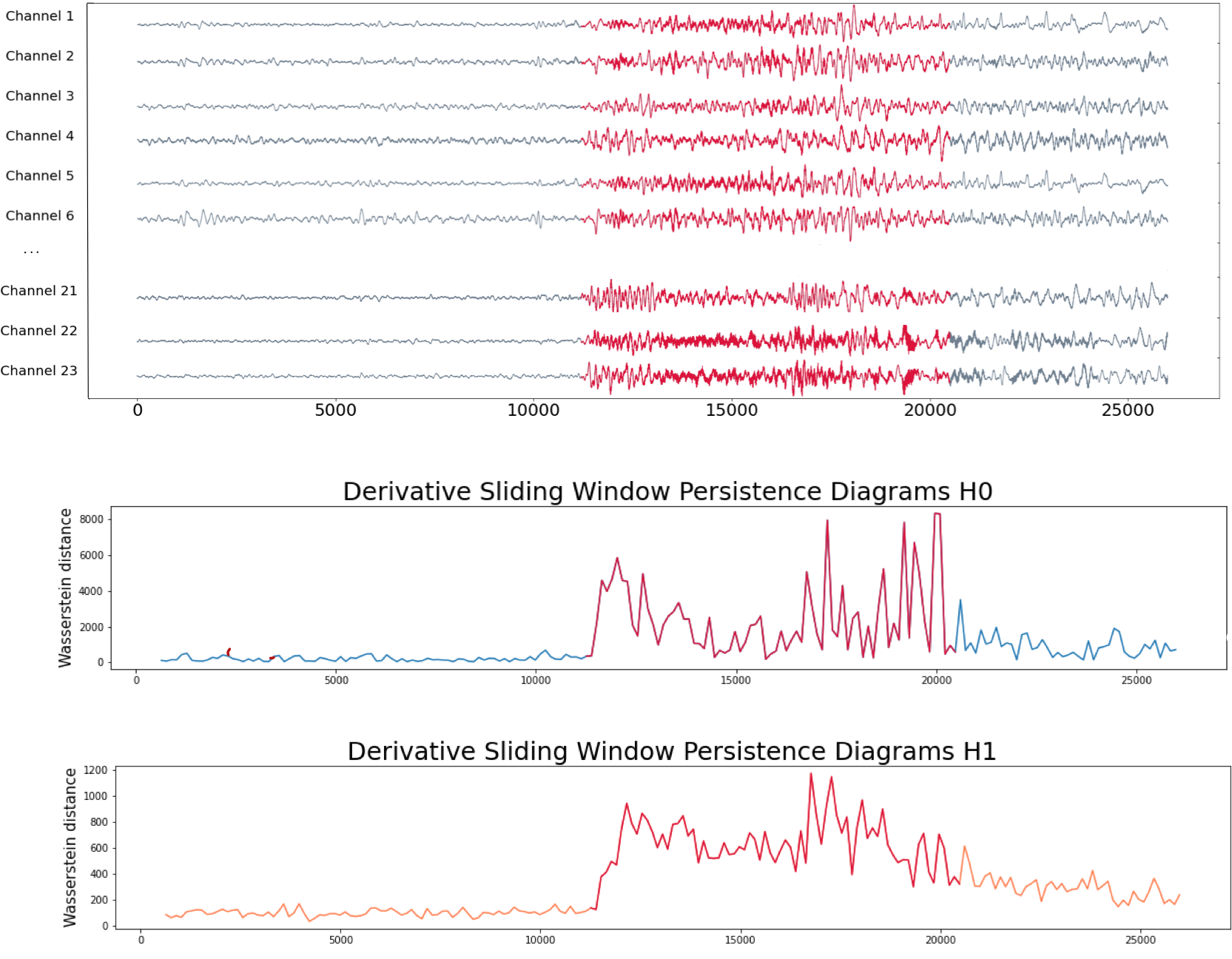
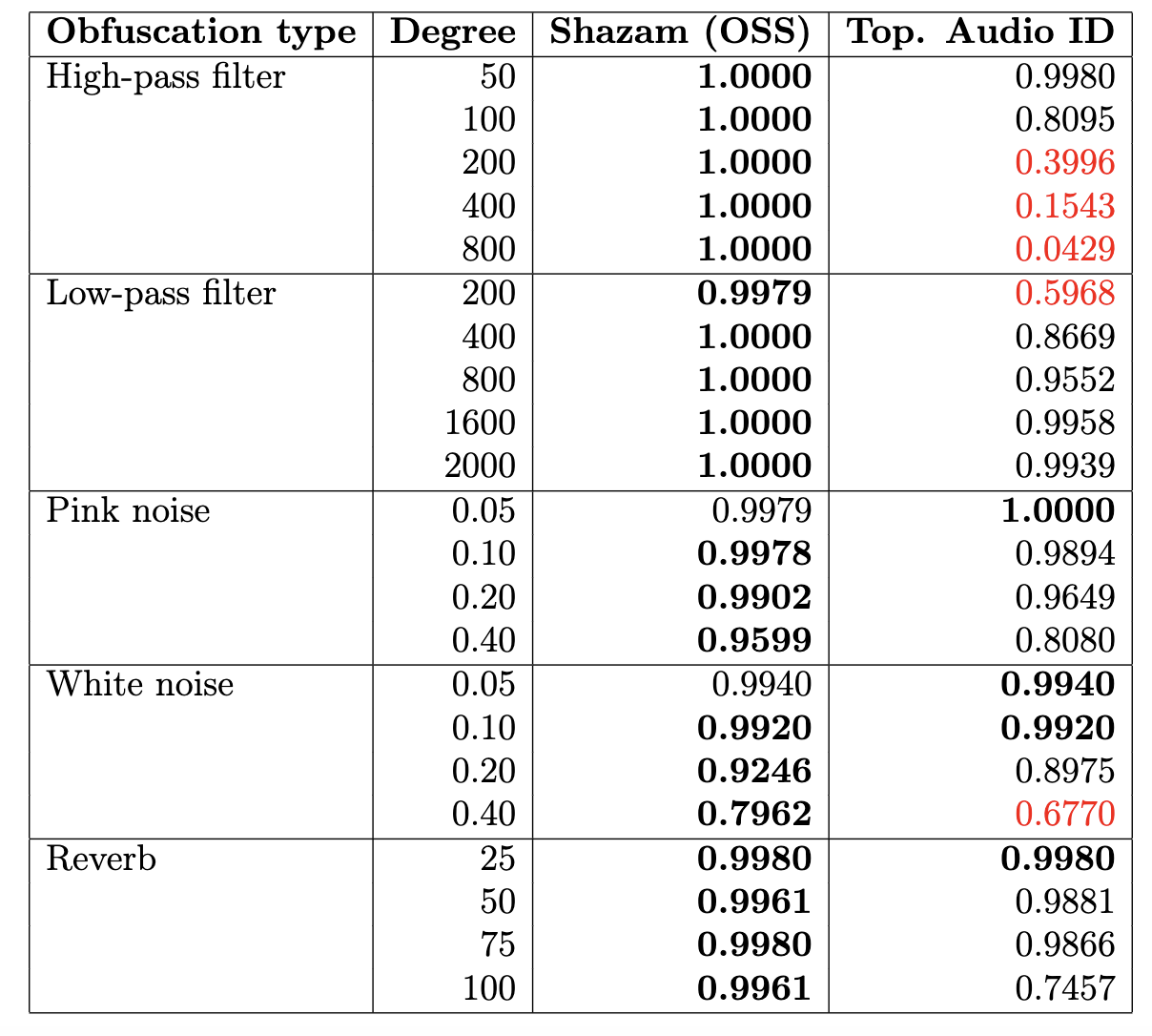
3. Topological Methods in Audio ID
Research collaboration with Spotify
W. Reise, X. Fernandez, M. Dominguez, H.A. Harrington, M. Beguerisse-Diaz. Topological fingerprints for audio identification. SIAM Journal on Mathematics of Data Science Vol. 6, Iss. 3 (2024)
3. Topological Methods in Audio ID
Research collaboration with Spotify
Problem: Given two audio tracks, identify whether they correspond to the same audio content.
$~~~~~~~~~~$
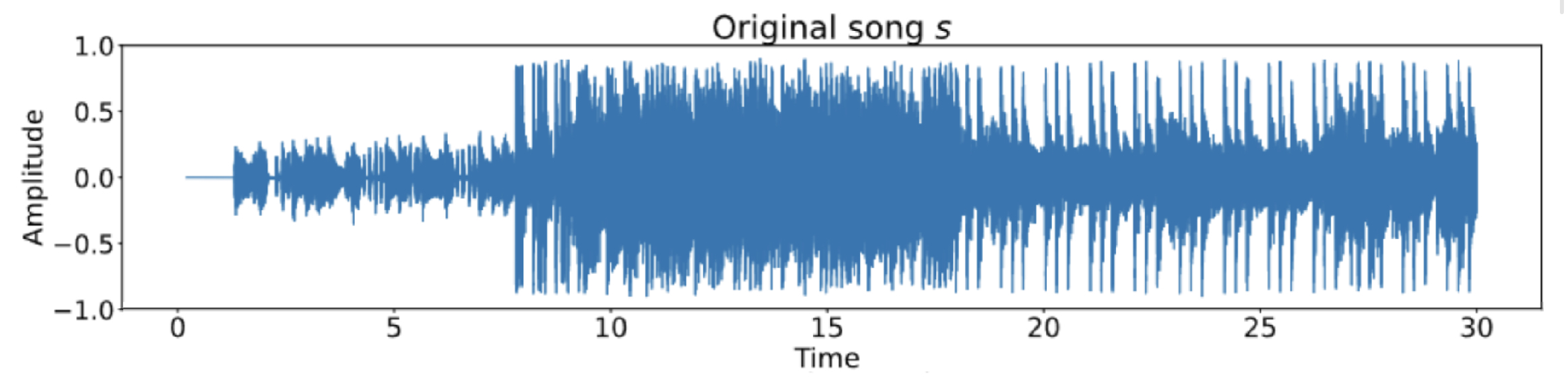
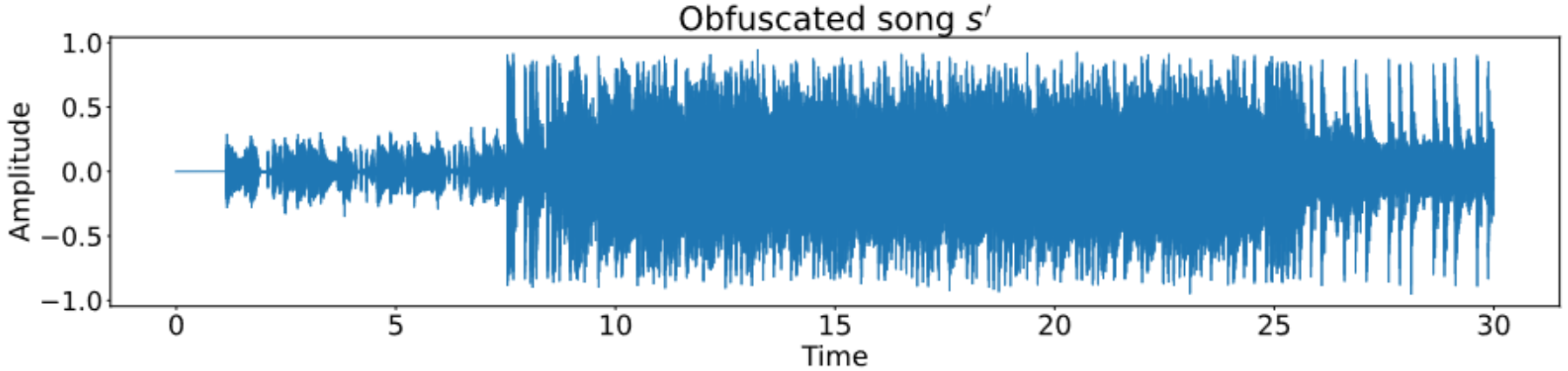
W. Reise, X. Fernandez, M. Dominguez, H.A. Harrington, M. Beguerisse-Diaz. Topological fingerprints for audio identification. SIAM Journal on Mathematics of Data Science Vol. 6, Iss. 3 (2024)
3. Topological Methods in Audio ID
Research collaboration with Spotify
3. Topological Methods in Audio ID
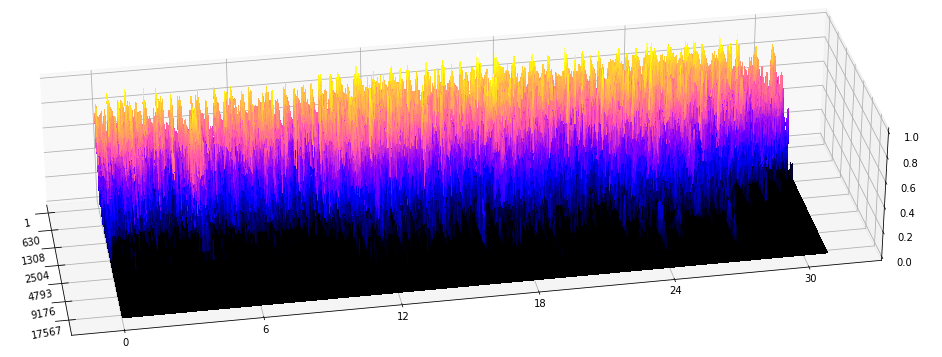
Research collaboration with Spotify
$~~~~~~~$
3. Topological Methods in Audio ID
Research collaboration with Spotify
3. Topological Methods in Audio ID
Research collaboration with Spotify

3. Topological Methods in Audio ID
Research collaboration with Spotify
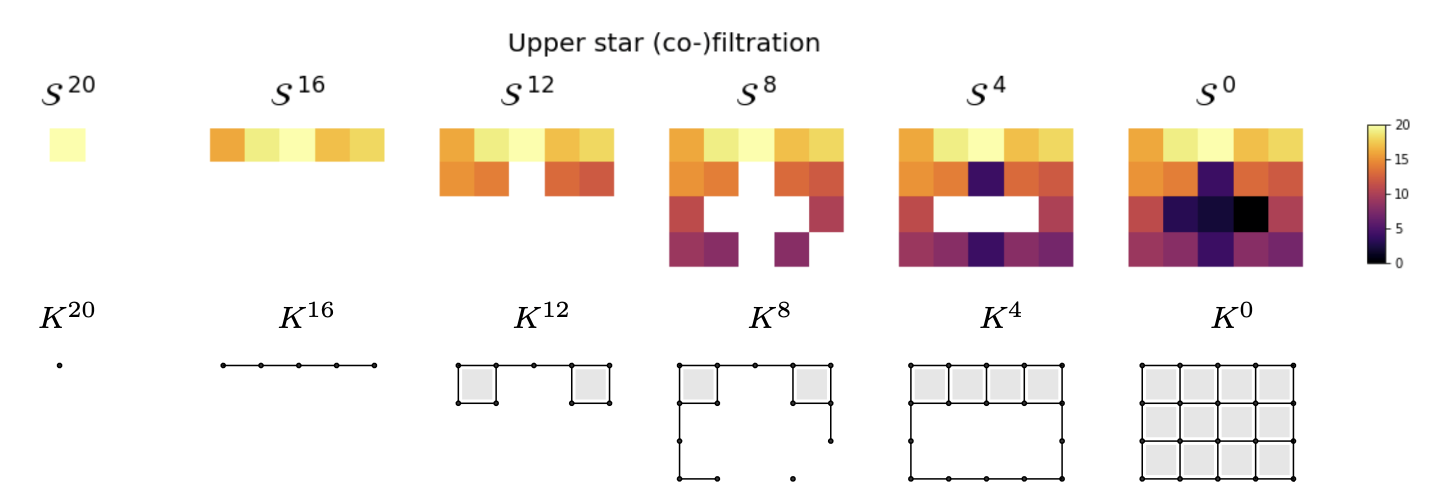
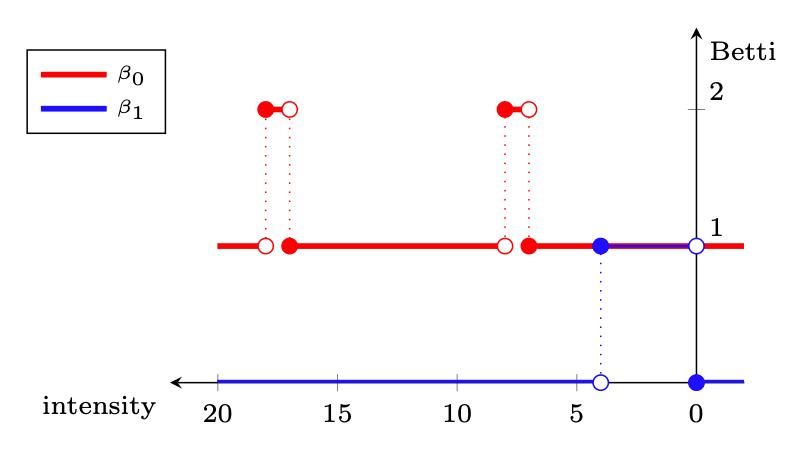
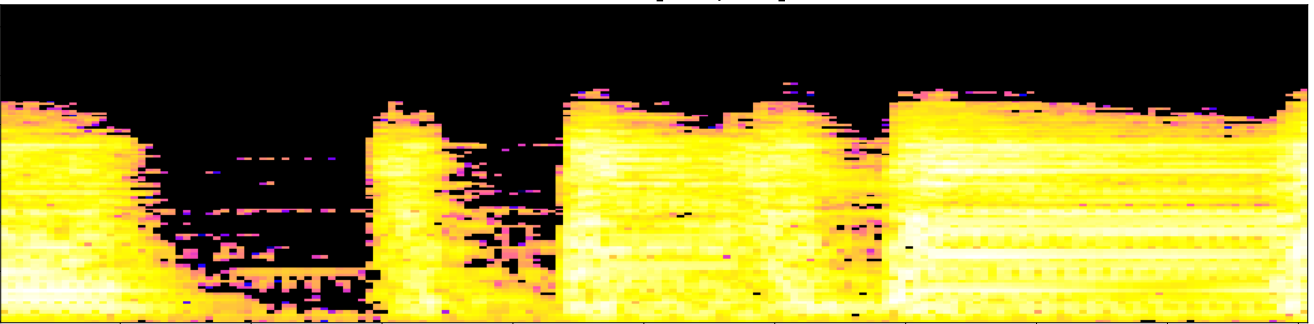
Given $s$ an audio track, we associate topological fingerprints via local Betti curves.


$~$
 $~$
$~$
 $~$
$~$
 $~$
$~$
 $~$
$~$
 $~~$
$~~$
 $~$
$~$
 $~$
$~$
 $~$
$~$
 $~$
$~$

$~$
$~~~~~~~~~~~t_0~~~~~~~~~~~~~~~~~t_1~~~~~~~~~~~~~~~~~~t_2~~~~~~~~~~~~~~~~~t_3~~~~~~~~~~~~~~~~~t_4~~~~~~\dots~~~~~~~~~~~t'_0~~~~~~~~~~~~~~~~~t'_1~~~~~~~~~~~~~~~~~t'_2~~~~~~~~~~~~~~~~t'_3~~~~~~~~~~~~~~~~t'_4~~\dots$
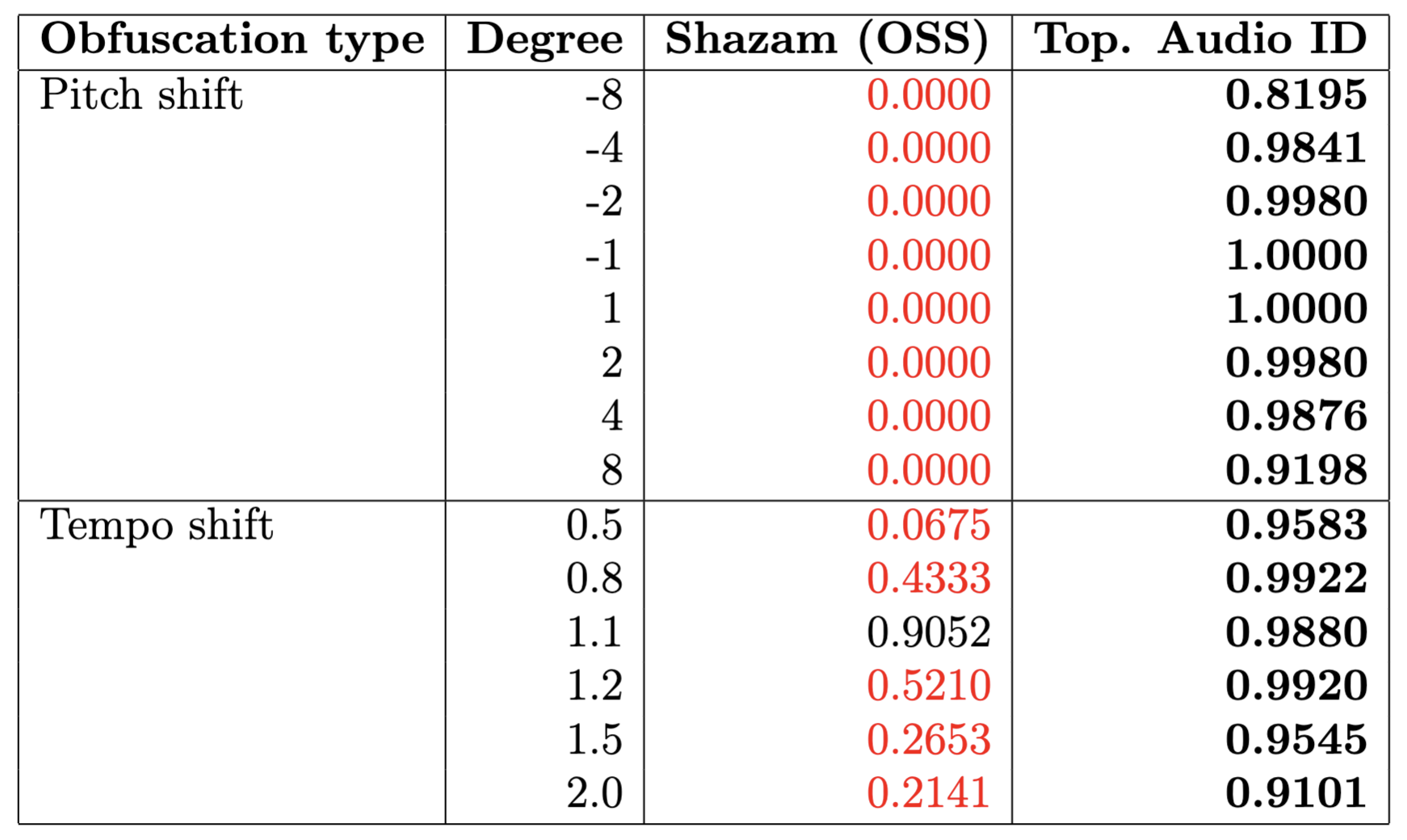
Correlation: 'Smells like teen spirit'. (30sec-30sec): 0.9896
3. Topological Methods in Audio ID
Research collaboration with Spotify
Future projects
Network science
Kuramoto models and synchronization
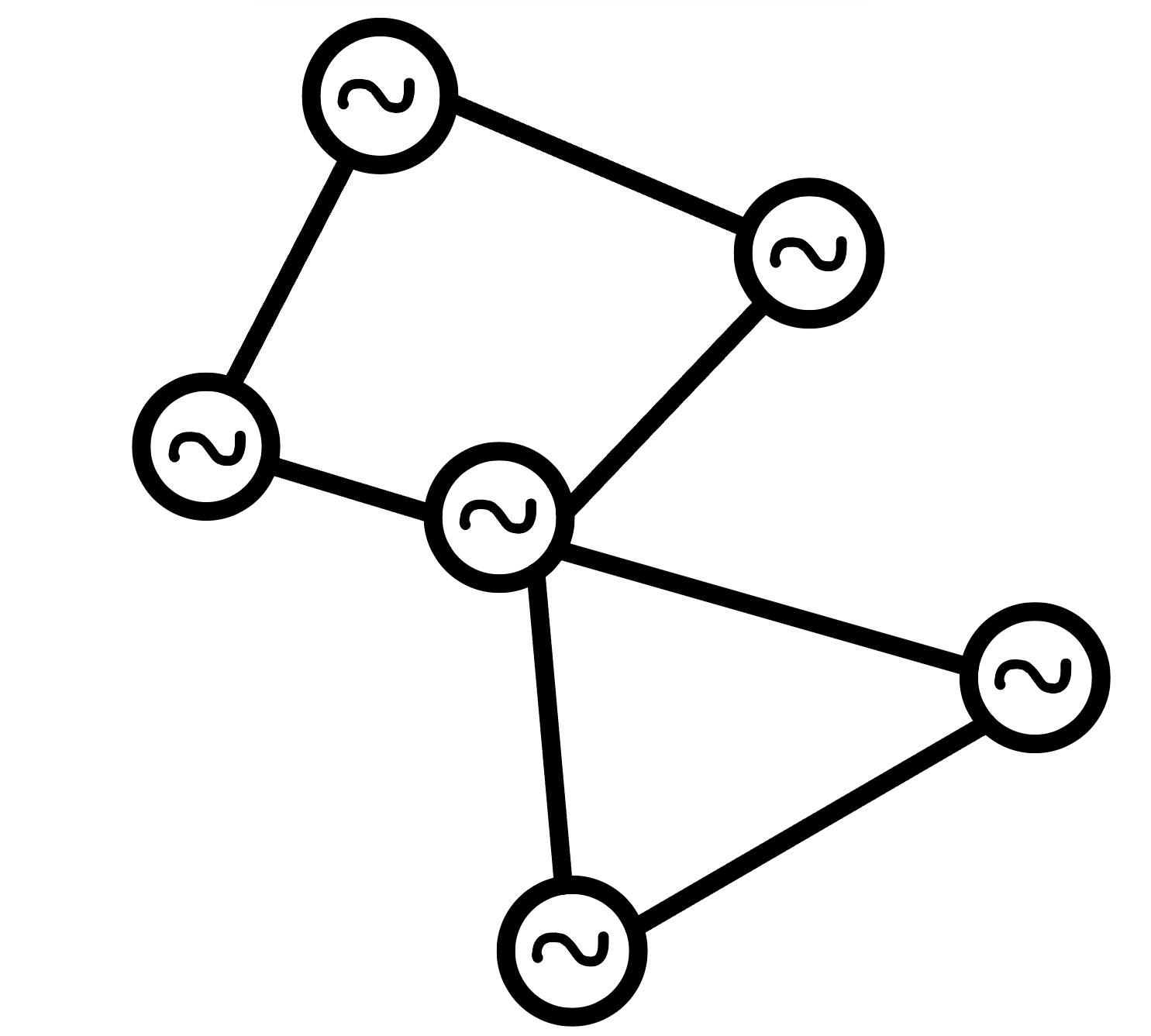
Kuramoto model
\[ \frac{d\theta_i}{dt} = \omega_i + \sum_{j=1}^{N} \omega_{ij}\sin(\theta_j - \theta_i), \quad i = 1, 2, \dots, N \]$~~~~~~$where:
- $ \theta_i(t) \in [0, 2\pi)$ is the phase of the \( i \)-th oscillator at time \( t \),
- $ \omega_i $ is the natural frequency of the \( i \)-th oscillator,
- $ \omega_{ij}$ strength of the coupling between oscillators $i$ and $j$,
- $ N $ is the total number of oscillators.
Network science
Kuramoto models and synchronization
Conjecture: The Kuramoto model on random geometric graphs over spaces with non-trivial homology does not synchronize.
Fluid dynamics
Dependence on initial conditions
Case study: Driven double gyre.Fluid dynamics
Dependence on initial conditions
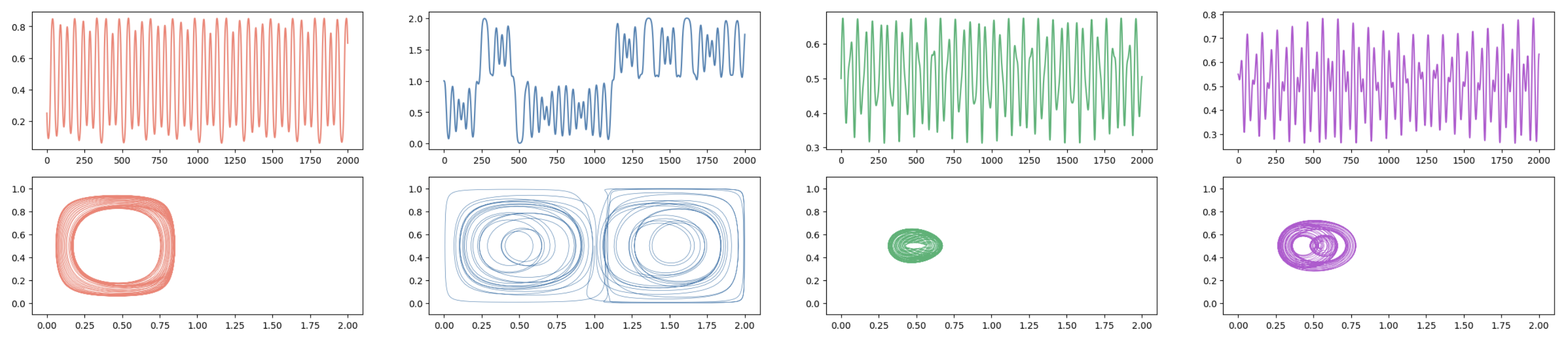
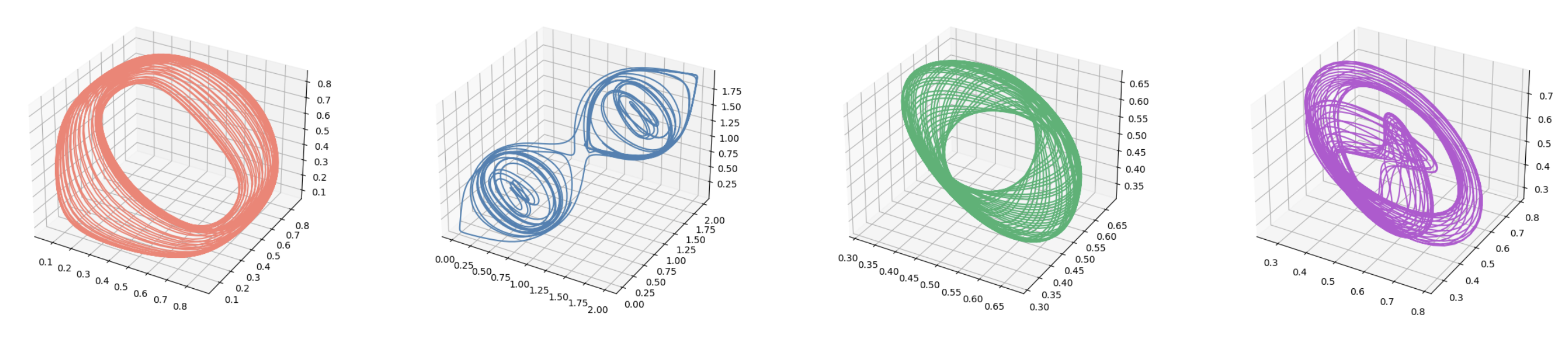
Fluid dynamics
Dependence on initial conditions


Persistence beyond homology
New topological invariants of data
Problem: Homology may fall short in capturing topological aspects of data.
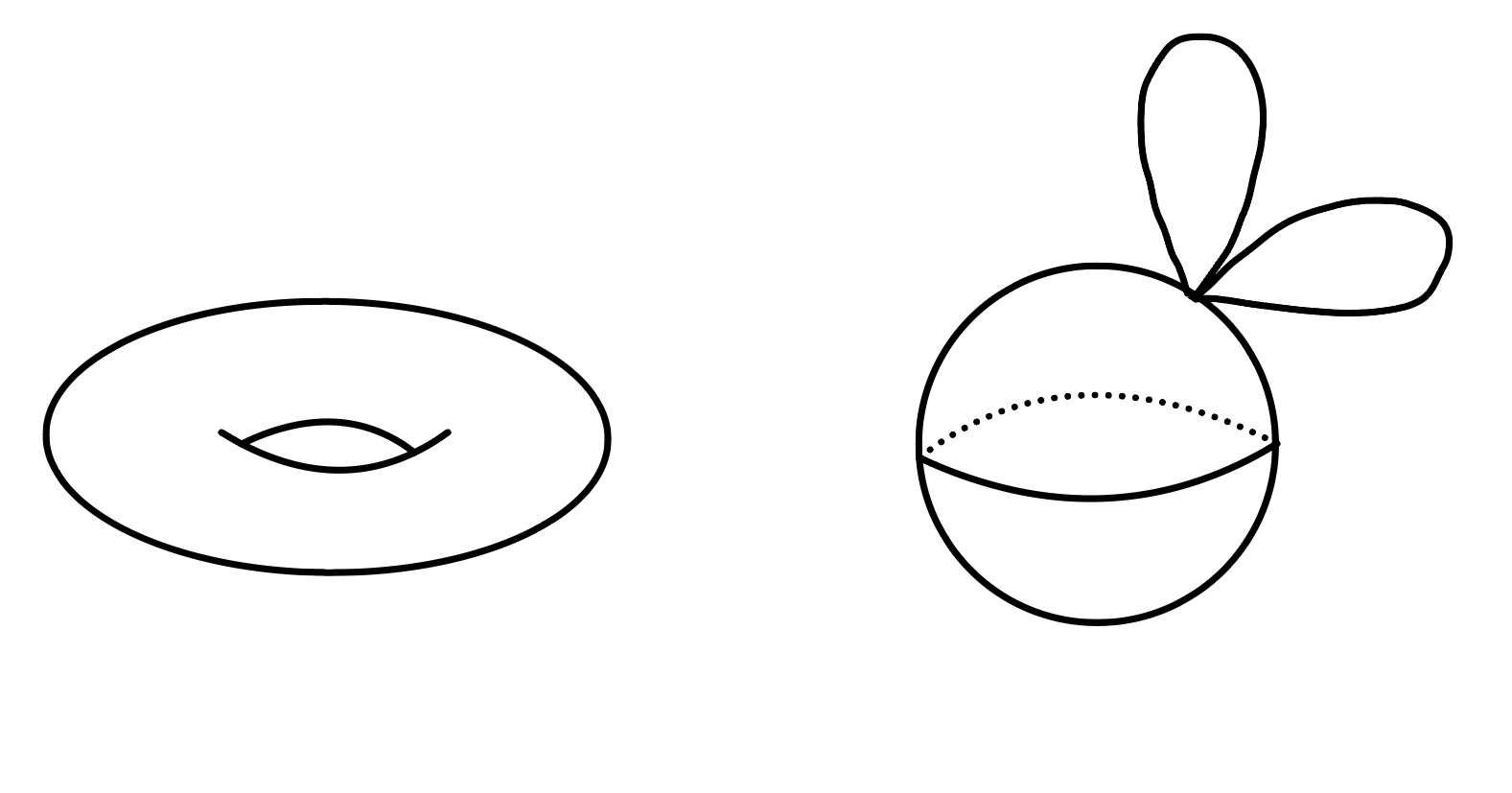
Persistence beyond homology
New topological invariants of data
Problem: Homology may fall short in capturing topological aspects of data.
- Efficient presentations of presentations of $\pi_1(K)$.
- Persistent fundamental group.
- Software in GAP.
Persistent knot invariants
- Fundamental group of the complement: $\pi_1(S^3\smallsetminus K)$
- Alexander polynomial.
- Reidemeister torsion.
Related to: X. Fernandez. Morse theory for group presentations. Transactions of the AMS. (2024)
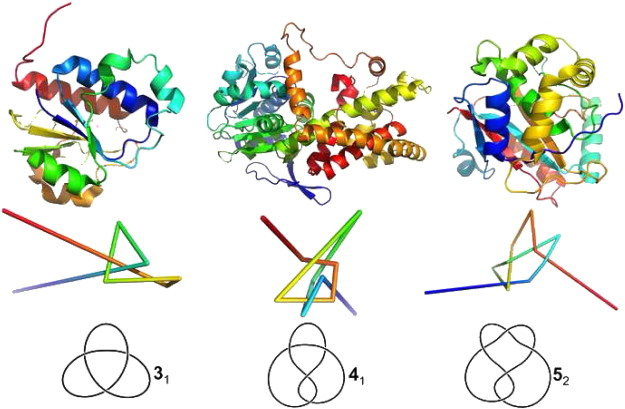
- Applications
- Classification of knotted proteins.
- Classification of chaotic attractors.
 $~~~~~~~~$
$~~~~~~~~$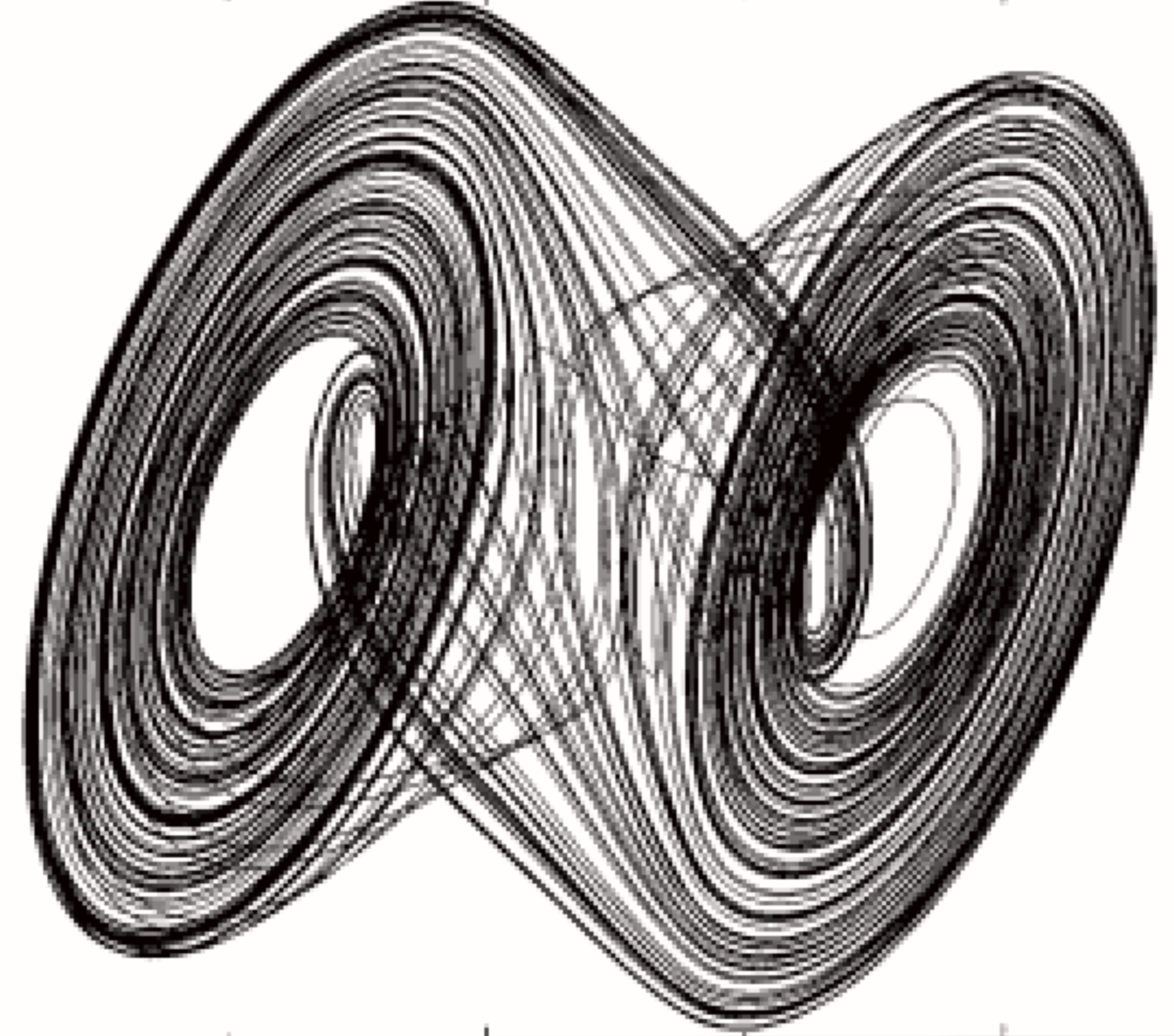
$~~$ Lorenz attractor$~~~~~~~~~~~~~~~~~~~$Chua attractor
TOPOLOGICAL DATA ANALYSIS

THANKS!