Density-based persistent homology &
applications to time series analysis
XIMENA FERNANDEZ
University of Oxford
Dresden-Oxford Maths meets Biology
Persistent homology in a nutshell
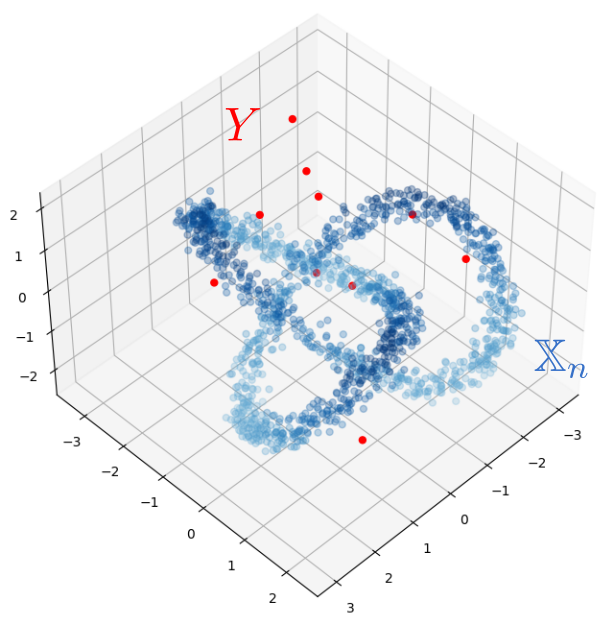
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Q: How to infer the homology of $X$ from $\mathbb{X}_n$?
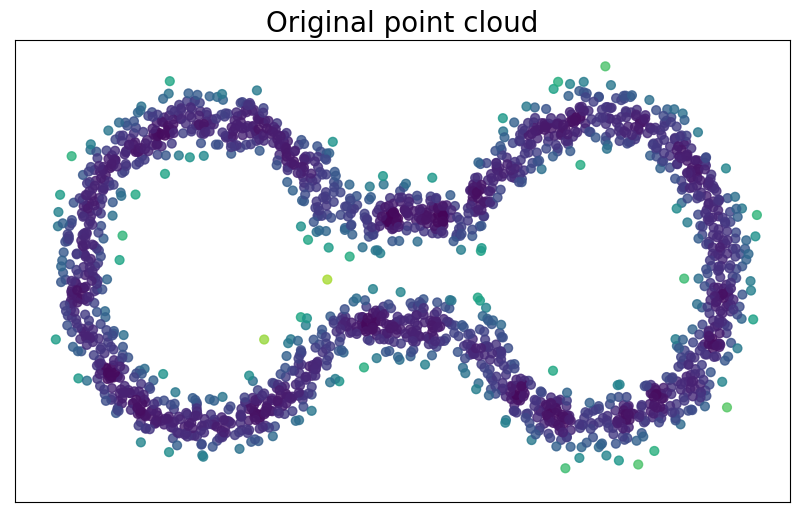
Point cloud
$\mathbb{X}_n \subset \mathbb{R}^D$

Evolving thickenings

Persistent homology in a nutshell
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Q: How to infer topological properties of $X$ from $\mathbb{X}_n$?
Point cloud
$\mathbb{X}_n \subset \mathbb{R}^D$

Evolving thickenings

Filtration of simplicial complexes

Persistent homology in a nutshell
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Q: How to infer topological properties of $X$ from $\mathbb{X}_n$?
Point cloud
$\mathbb{X}_n \subset \mathbb{R}^D$

Filtration of simplicial complexes

Persistence diagram

Persistent homology
Euclidean distanceMetric space: $(\mathbb X_n, d_E)\sim (\mathcal M, d_E)$
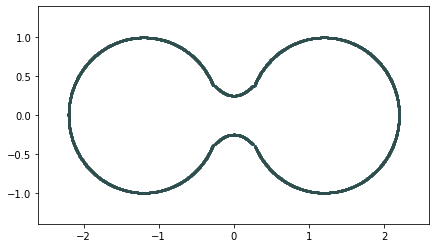

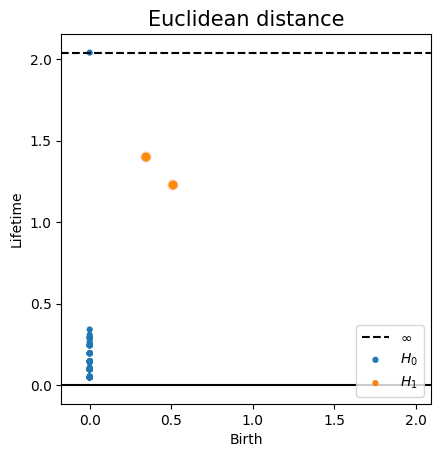
Persistent homology
Geodesic distanceMetric space: $(\mathbb X_n, d_{kNN})\sim (\mathcal M, d_\mathcal{M})~~~$


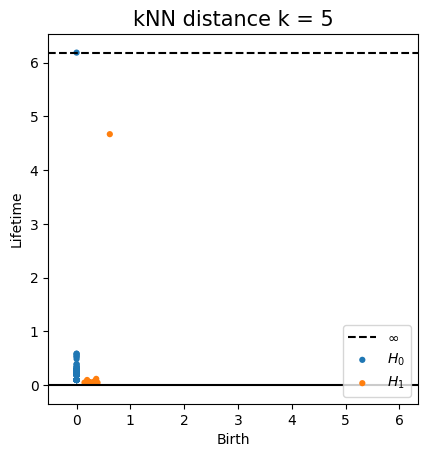
Persistent homology
Geodesic distanceMetric space: $(\mathbb X_n, d_{kNN})\sim (\mathcal M, d_\mathcal{M})$

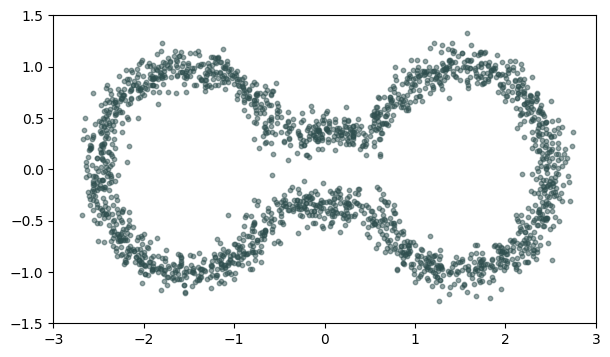
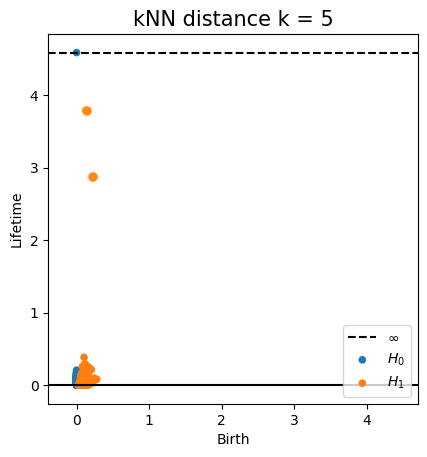
The metric structure
Desired properties of a metric:$\checkmark$ 'Independence' on the ambient space (intrinsic).
$\checkmark$ Robustness to noise/outliers.
Density-based geometry
Density-based geometry



Density-based geometry
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ be a finite sample.

Density-based geometry
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ be a finite sample.
Assume that:
- $\mathbb{X}_n$ is a sample of a compact manifold $\mathcal M$ of dimension $d$.
- The points are sampled according to a density $f\colon \mathcal M\to \mathbb R$.

Density-based geometry
(Hwang, Damelin & Hero, 2016)
Let $\mathcal M \subseteq \mathbb{R}^D$ be a manifold and let $f\colon\mathcal{M}\to \mathbb{R}_{>0}$ be a smooth density.
For $q>0$, the deformed Riemannian distance* in $\mathcal{M}$ is \[d_{f,q}(x,y) = \inf_{\gamma} \int_{I}\frac{1}{f(\gamma_t)^{q}}||\dot{\gamma}_t|| dt \] over all $\gamma:I\to \mathcal{M}$ with $\gamma(0) = x$ and $\gamma(1)=y$.
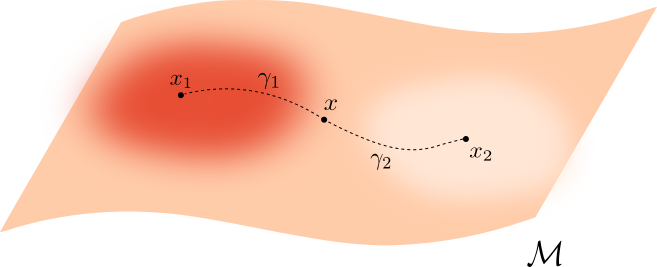
* Here, if $g$ is the inherited Riemannian tensor, then $d_{f,q}$ is the Riemannian distance induced by $g_q= f^{-2q} g$.
Fermat distance
(Mckenzie & Damelin, 2019) (Groisman, Jonckheere & Sapienza, 2022)
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ be a finite sample.
For $p> 1$, the Fermat distance between $x,y\in \mathbb{R}^D$ is defined by \[ d_{\mathbb{X}_n, p}(x,y) = \inf_{\gamma} \sum_{i=0}^{r}|x_{i+1}-x_i|^{p} \] over all paths $\gamma=(x_0, \dots, x_{r+1})$ of finite length with $x_0=x$, $x_{r+1} = y$ and $\{x_1, x_2, \dots, x_{r}\}\subseteq \mathbb{X}_n$.

Fermat distance

Fermat distance


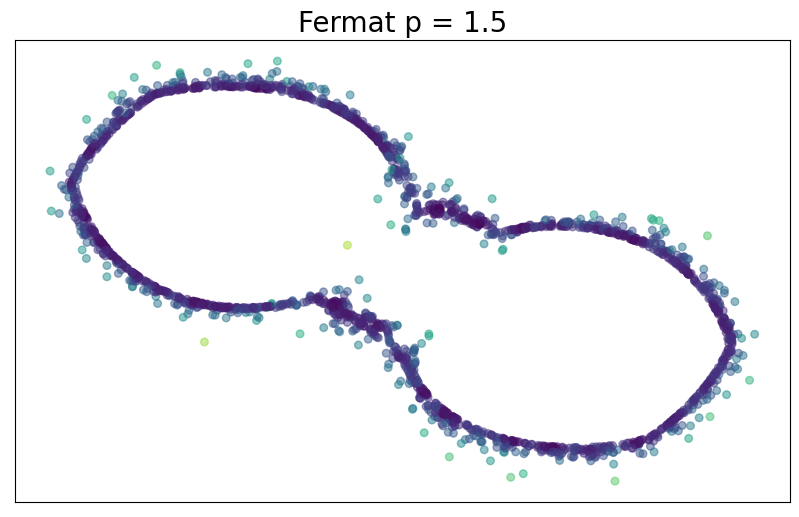
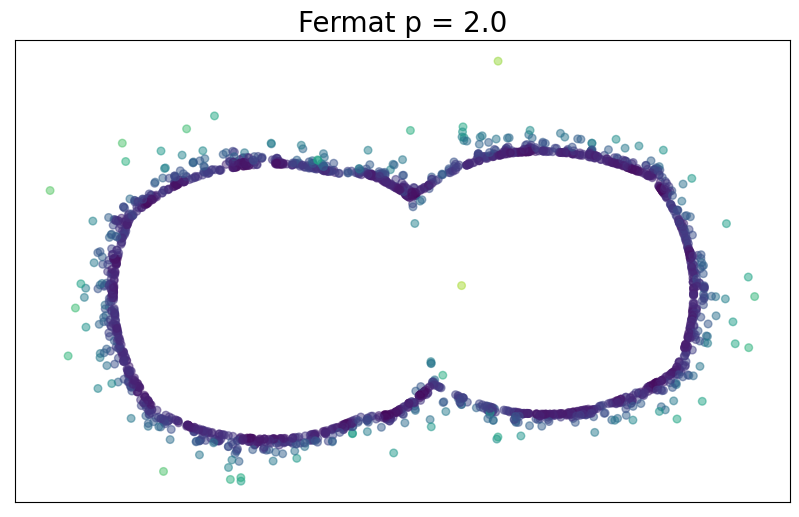
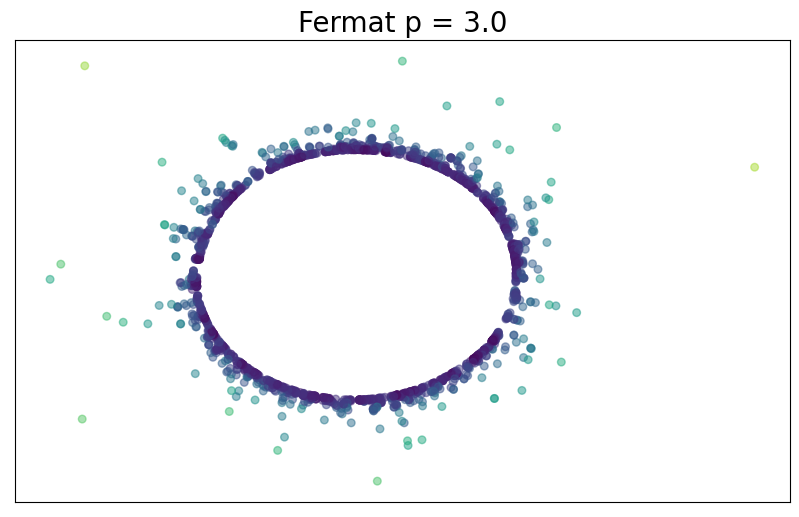
Convergence results
(F., Borghini, Mindlin & Groisman, 2023)
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]
Convergence results
(F., Borghini, Mindlin & Groisman, 2023)
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p})\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]
$\Downarrow$\[\mathrm{dgm}(\mathrm{Filt}(\mathbb{X}_n, {C(n,p,d)} d_{\mathbb{X}_n,p}))\xrightarrow[n\to \infty]{B}\mathrm{dgm}(\mathrm{Filt}(\mathcal{M}, d_{f,q})) ~~~ \text{ for } q = (p-1)/d\]
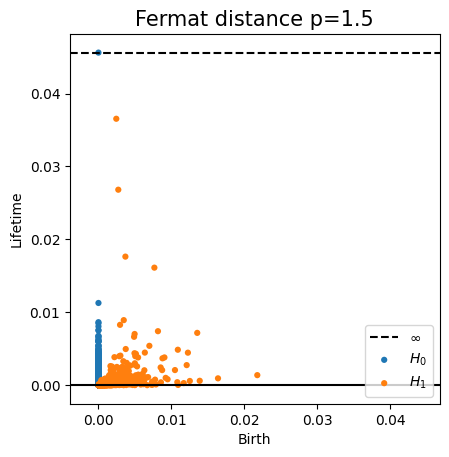
Fermat-based persistence diagrams

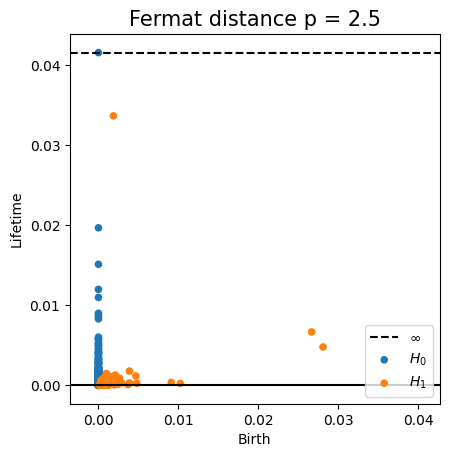
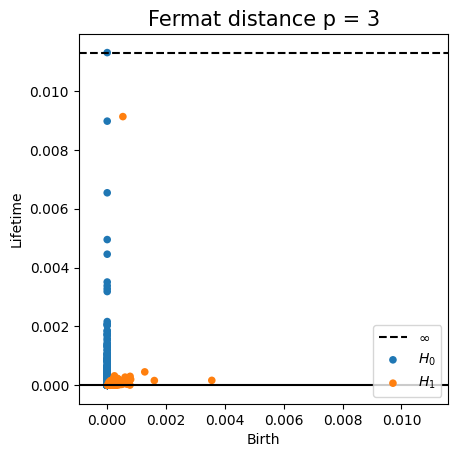
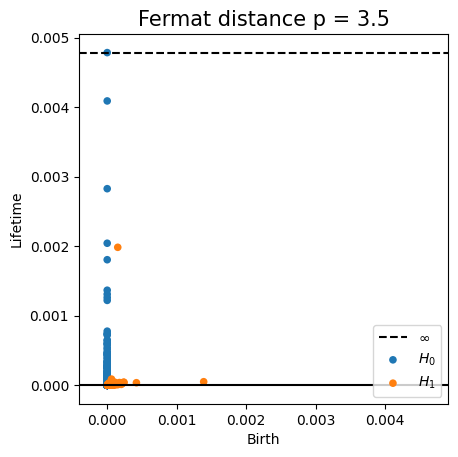
Fermat-based persistence diagrams


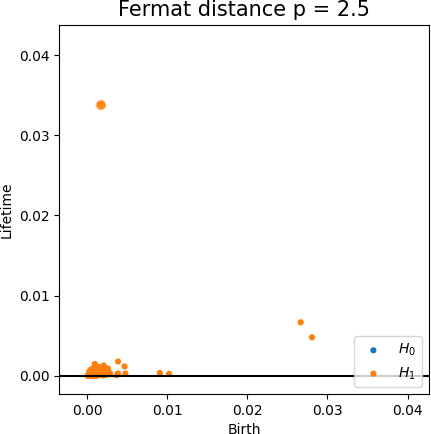
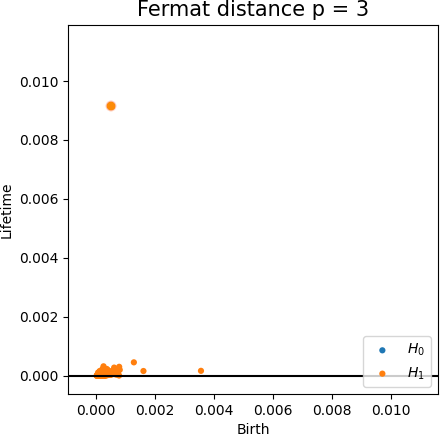
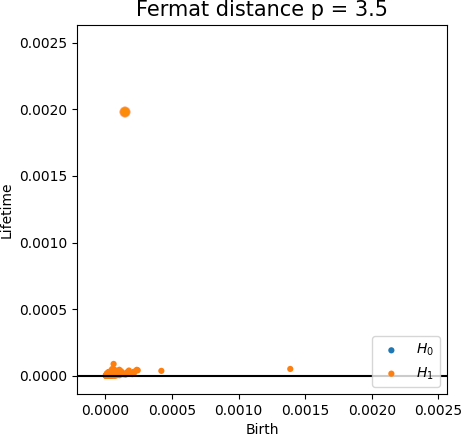
Fermat-based persistence diagrams
Robustness to outliers
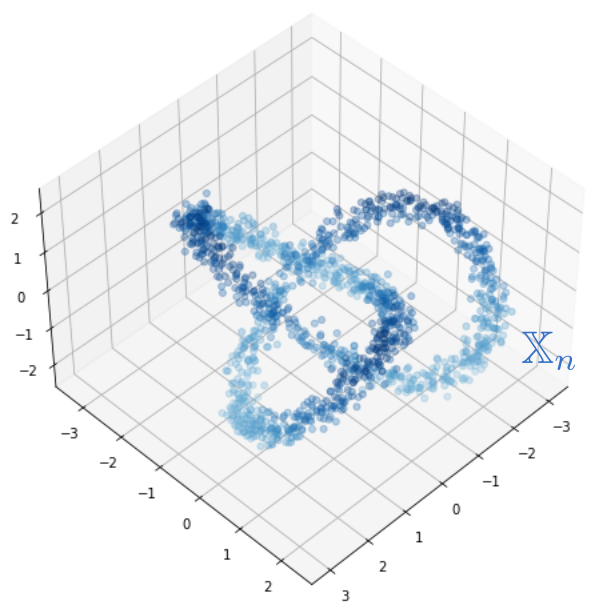
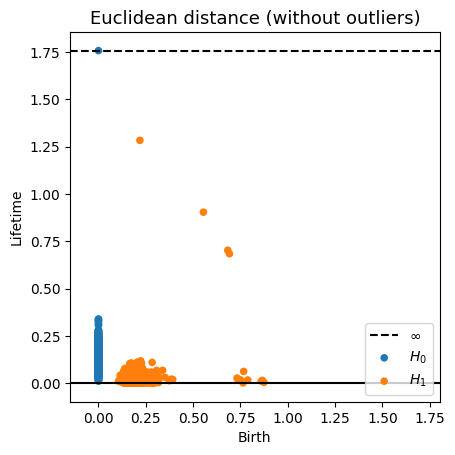
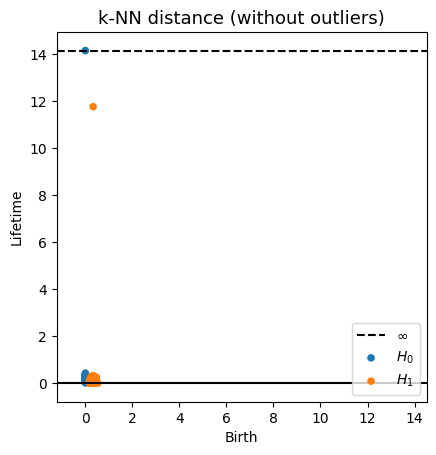
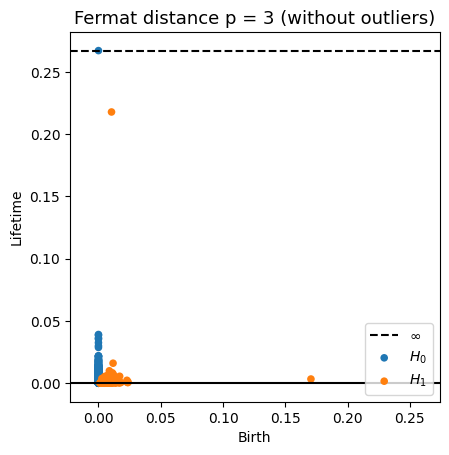
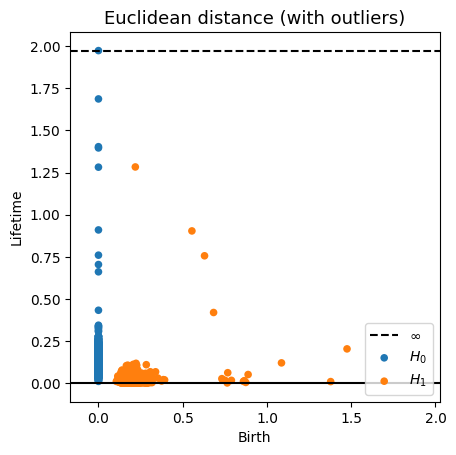
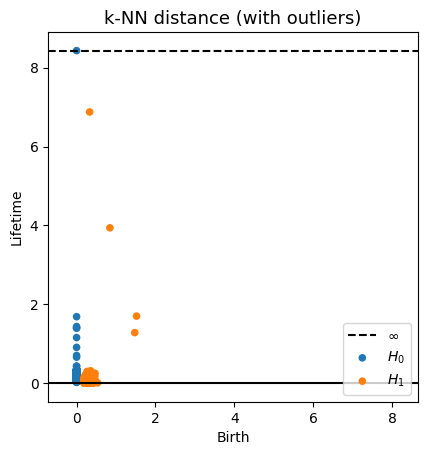
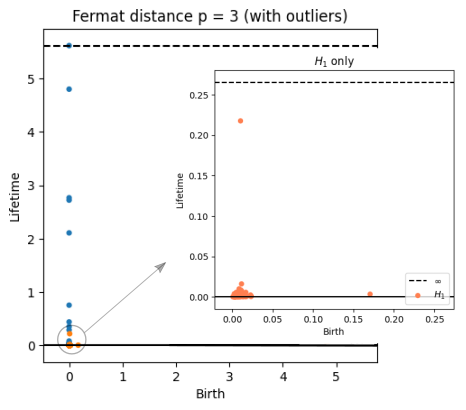
Time series Analysis
Topological analysis of time series
- Signal:
$\varphi:\mathbb R \to \mathbb{R}$

We assume that $\varphi$ is an observation of an underlying dynamical system $(\mathcal M, \phi)$, with $\mathcal M$ a topological space and $\phi\colon \mathbb R \times \mathcal M\to \mathcal M$ the evolution function.
That is, there exist an observation function $F:\mathcal M\to \mathbb R$ and an initial state $x_0\in \mathcal M$ such that \begin{align}\varphi = \varphi_{x_0}:\mathbb{R}&\to \mathbb{R}\\ t&\mapsto F(\phi_t(x_0)) \end{align}
Topological analysis of time series
- Signal:
$\varphi:\mathbb R \to \mathbb{R}$

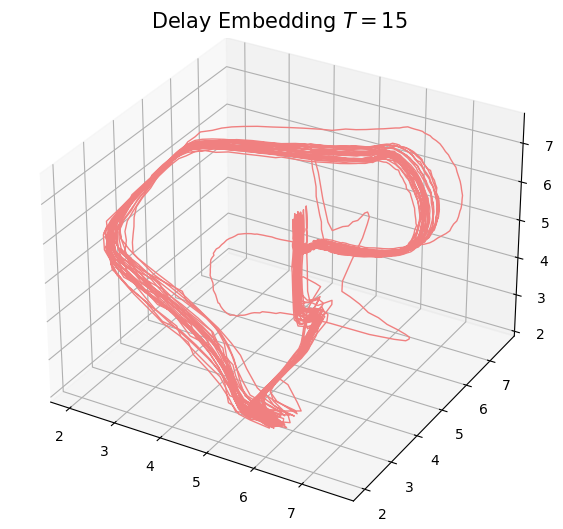
- Delay embedding: Given $T$ the time delay and $D$ the embedding dimension. \[\mathcal{M}_{T,D} = \{\big(\varphi(t), \varphi(t+T), \varphi(t+2 T) \dots, \varphi(t+(D-1)T)\big): t\in \mathbb R\}\subseteq \mathbb{R}^D\]
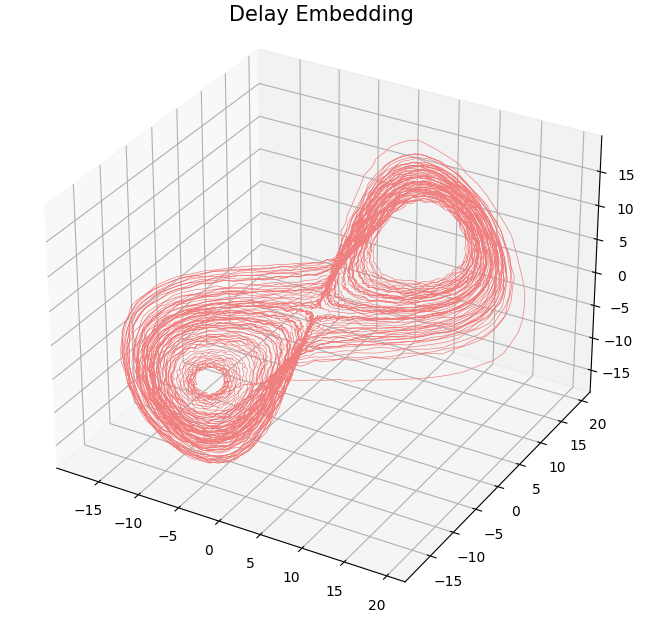
Topological analysis of time series
- Signal:
$\varphi:\mathbb R \to \mathbb{R}$

- Delay embedding: Given $T$ the time delay and $D$ the embedding dimension. \[\mathcal{M}_{T,D} = \{\big(\varphi(t), \varphi(t+T), \varphi(t+2 T) \dots, \varphi(t+(D-1)T)\big): t\in \mathbb R\}\subseteq \mathbb{R}^D\]
- Limit set: Given $(\mathcal M, \phi)$ a dynamical system and $x_0\in \mathcal M$, \[\mathcal A_{x_0} = \{x\in \mathcal M: \exists t_i\to \infty \text { with } \phi_{t_i}(x_0)\to x\}.\]

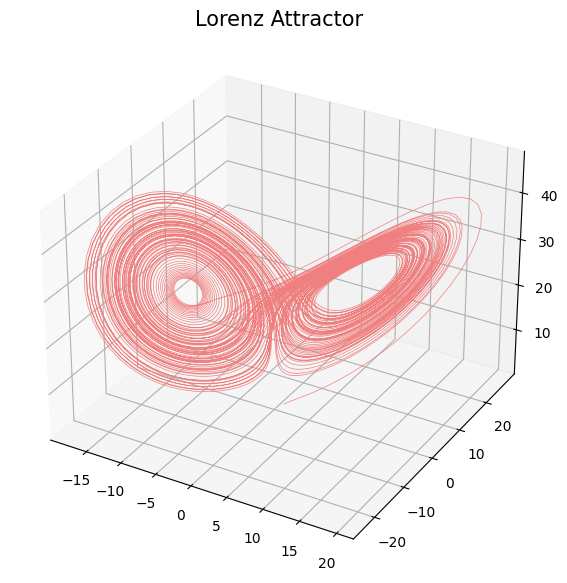
Topological analysis of time series
- Signal:
$\varphi:\mathbb R \to \mathbb{R}$

- Delay embedding: Given $T$ the time delay and $D$ the embedding dimension. \[\mathcal{M}_{T,D} (\phi) = \{\big(\varphi(t), \varphi(t+T), \varphi(t+2 T) \dots, \varphi(t+(D-1)T)\big): t\in \mathbb R\}\subseteq \mathbb{R}^D\]
- Limit set: Given $(\mathcal M, \phi)$ a dynamical system and $x_0\in \mathcal M$, \[\mathcal A_{x_0} = \{x\in \mathcal M: \exists t_i\to \infty \text { with } \phi_{t_i}(x_0)\to x\}.\]
- Theorem (Takens).* Let $\mathcal{M}$ be a smooth, compact, Riemannian manifold. Let $T> 0$ be a real number and let $D > 2 \mathrm{dim}(\mathcal{M})$
be an integer. Then, for generic $\phi \in C^2(\mathbb{R} \times \mathcal{M}, \mathcal{M})$, $F\in C^2(\mathcal{M}, \mathbb{R})$ and $x_0\in \mathcal M$, if $\varphi_{x_0} = F(\phi_\bullet(x_0))$ is an observation of $(\mathcal M, \phi)$, then
the limit set $\mathcal A_{x_0}$ is 'diffeomorphic'$^{**}$ to the delay embedding $\mathcal{M}_{T,D} (\varphi_{x_0})$.
** There exists $\psi:\mathcal M\to \mathbb R^{D}$ an embedding such that $\psi|_{\mathcal A_{x_0}}: \mathcal A_{x_0}\to \mathcal{M}_{T,D} (\varphi_{x_0})$ is a bijection.
*Corollary 5, Detecting strange attractors in tubulence, F. Takens, 1971.
Anomaly detection
Electrocardiogram
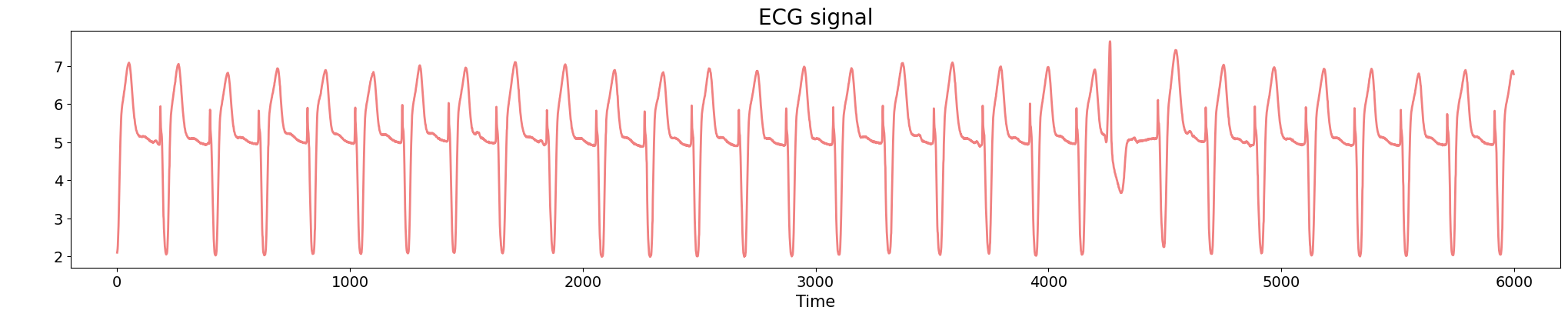
Source data: PhysioNet Database https://physionet.org/about/database/
Anomaly detection
Electrocardiogram

Anomaly detection
Electrocardiogram
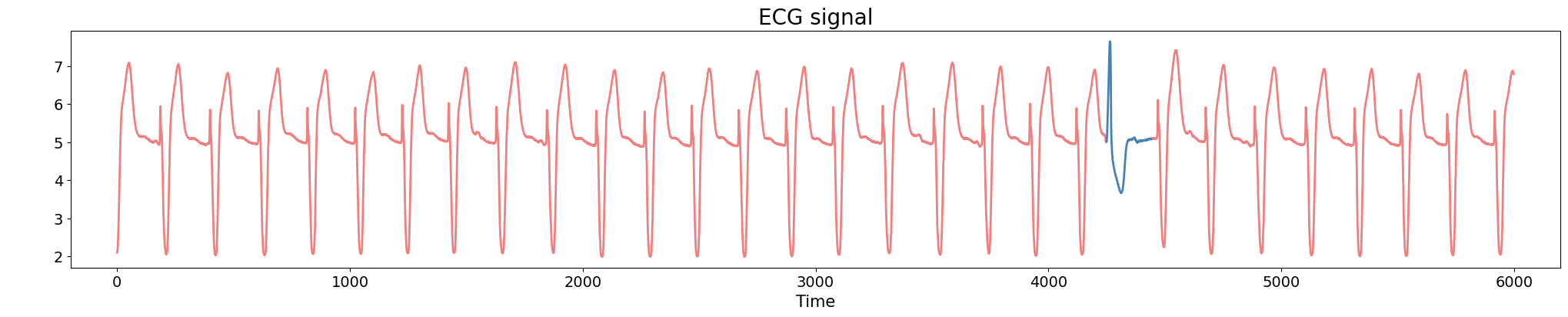
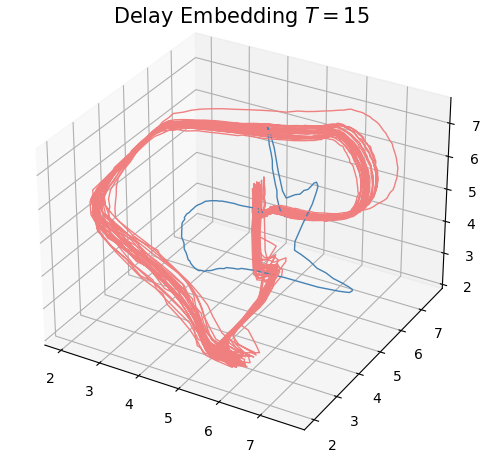
Anomaly detection
Electrocardiogram


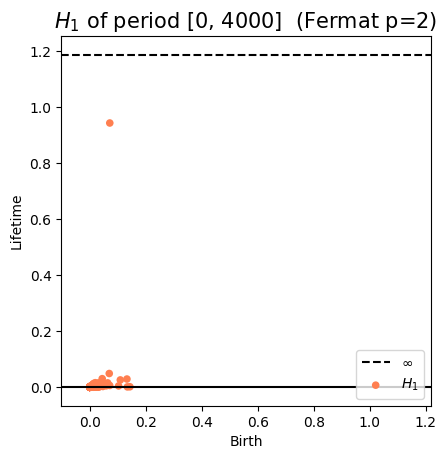
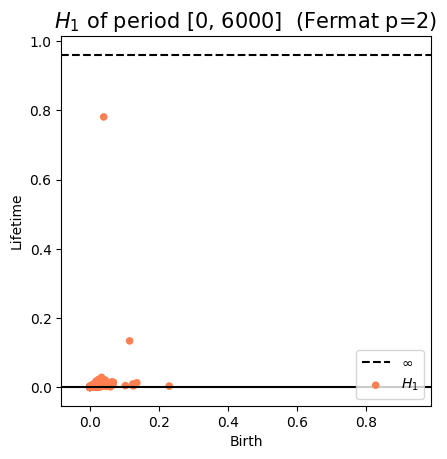
Anomaly detection
Electrocardiogram
 \[t\mapsto \mathcal{D}_t\]
Approximate Derivative: $\dfrac{d_{B}(\mathcal{D}_t, \mathcal{D}_{t-\varepsilon})}{\varepsilon}$
\[t\mapsto \mathcal{D}_t\]
Approximate Derivative: $\dfrac{d_{B}(\mathcal{D}_t, \mathcal{D}_{t-\varepsilon})}{\varepsilon}$

Change-points detection
Birdsongs

Source data: Private experiments. Laboratory of Dynamical Systems, University of Buenos Aires.
Change-points detection
Birdsongs

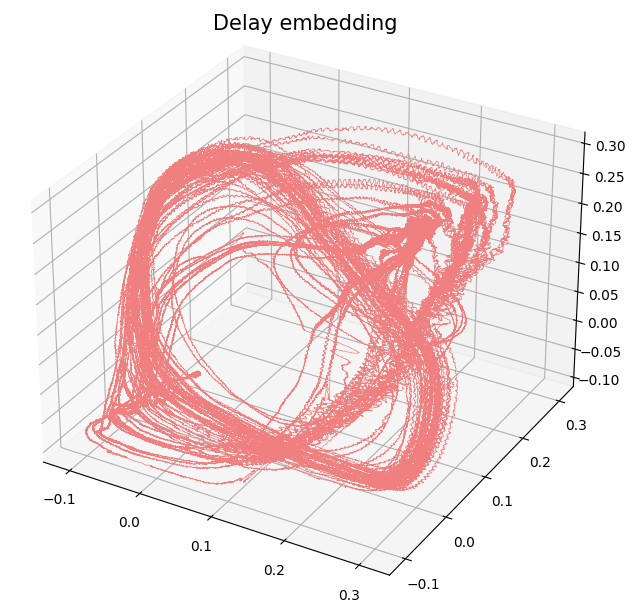
Change-points detection
Birdsongs


Change-points detection
Birdsongs

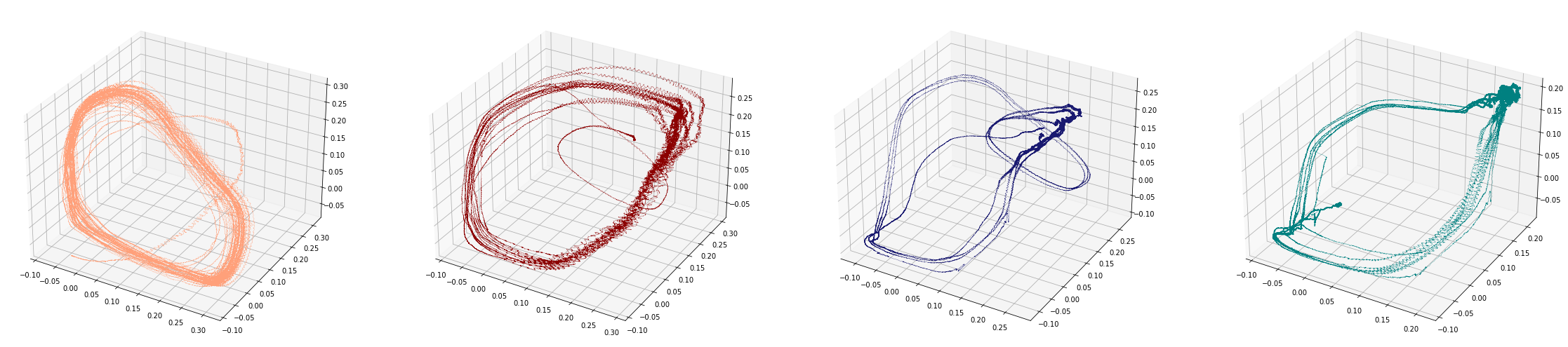

Change-points detection
Birdsongs


Epileptic seizure detection
EEG
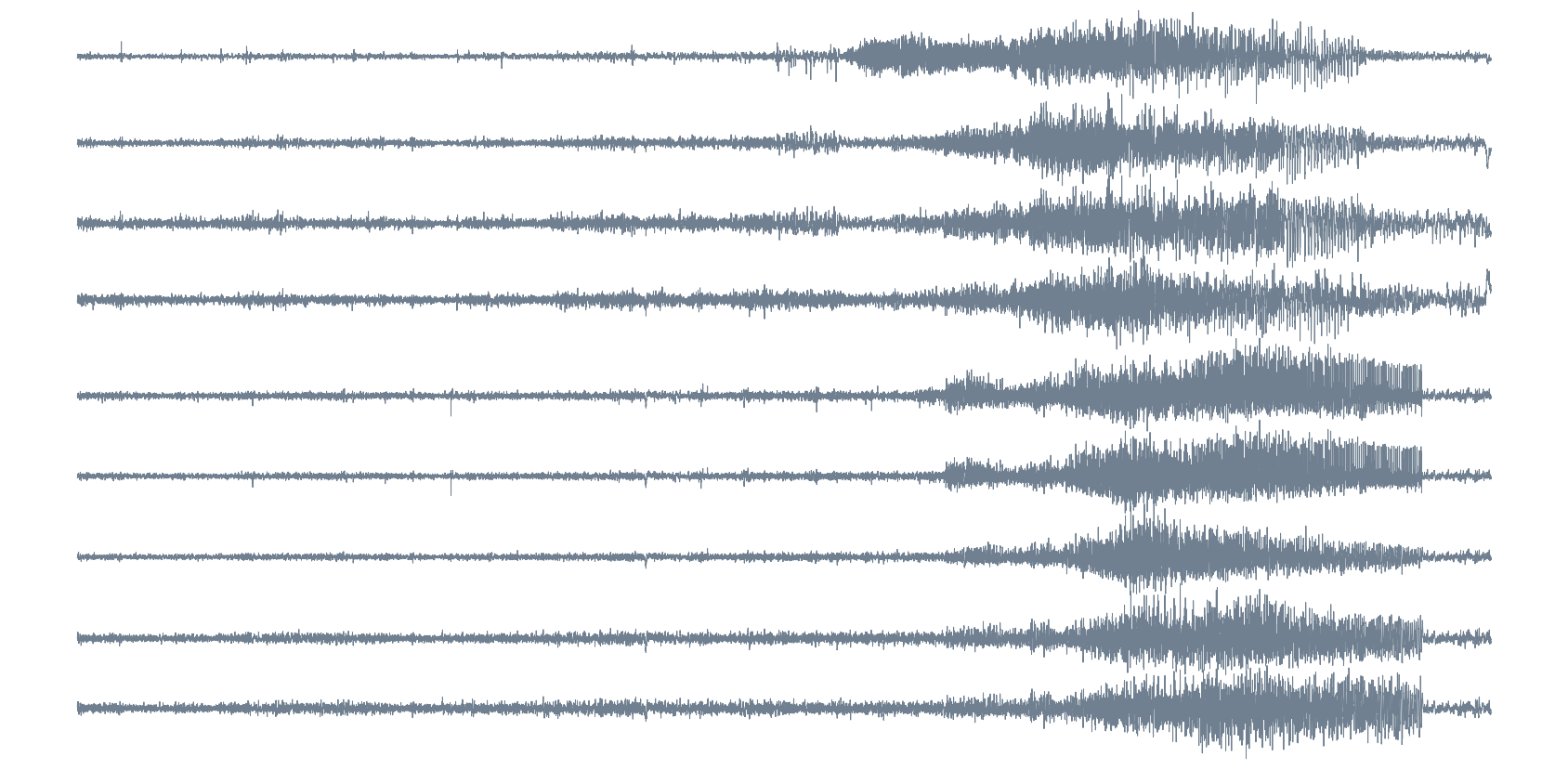
Epileptic seizure detection
EEG

Epileptic seizure detection
EEG

Epileptic seizure detection
EEG

Epileptic seizure detection
EEG
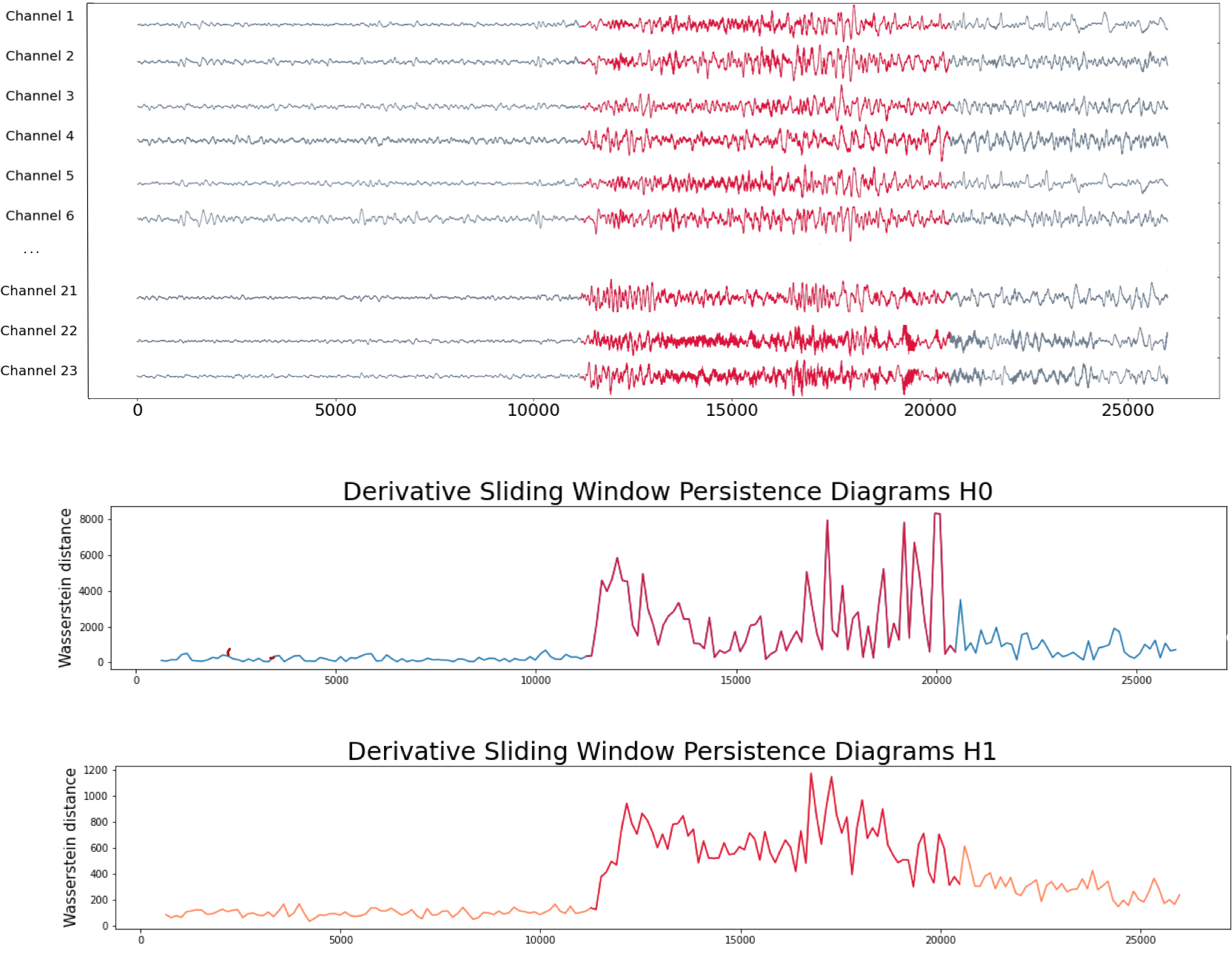
References
- X. Fernandez, E. Borghini, G. Mindlin, P. Groisman. Intrinsic persistent homology via density-based metric learning. Journal of Machine Learning Research 24(75):1−42 (2023).
- X. Fernandez, D. Mateos Topological biomarkers for real-time detection of epileptic seizures. arXiv:2211.02523 (2022).
- Github Repositories: ximenafernandez/intrinsicPH $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$ximenafernandez/epilepsy
- Tutorial: Intrinsic persistent homology. AATRN Youtube Channel (2021)
- Python Library: fermat