Density-based metric learning &
applications to topological data analysis
XIMENA FERNANDEZ
Durham University
Joint work with E. Borghini, G. Mindlin & P. Groisman.
29th Nordic Congress of Mathematicians
Geometric and Topological Methods in Computer Science
Aalborg University - 6th July 2023
Motivation
The shape of data
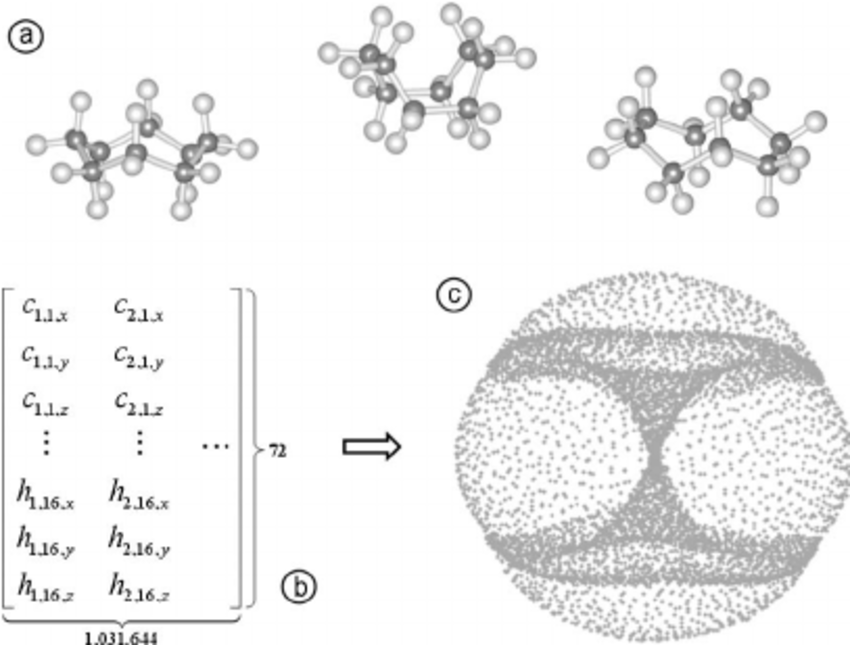
Martin et al. Topology of cyclo-octane energy landscape. J Chem Phys. 2010
Barbensi et al. A topological eslection of folding Pathways from native states of knotted proteins. Symm. 2021


Gardner et al. Toroidal topology of population activity in grid cells. Nature. 2022
The metric structure
$(\mathbb X_n, d)$ metric space.
The metric structure
$(\mathbb X_n, d)$ metric space.- Clustering.
$K$-medoids method aims to partition $\mathbb X_n$ in $S_1, S_2, \dots, S_k$ with associated $x_{S_i}\in S_i$ to minimize \[\sum_{i=1}^k\sum_{x\in S_i}d(x, x_{S_i})\]


The metric structure
$(\mathbb X_n, d)$ metric space.- Clustering.
$K$-medoids method aims to partition $\mathbb X_n$ in $S_1, S_2, \dots, S_k$ with associated $x_{S_i}\in S_i$ to minimize \[\sum_{i=1}^k\sum_{x\in S_i}d(x, x_{S_i})\] - Dimensionality reduction.
Multi-dimensional scaling (MDS) aims to find a projection $p:(\mathbb X_n, d)\to (\mathbb R^k, d_E)$ that minimizes \[\sum_{i\neq j=1,\dots,n} d(x_i,x_j)-d_E\big(p(x_i), p(x_j)\big)\]

The metric structure
$(\mathbb X_n, d)$ metric space.- Clustering.
$K$-medoids method aims to partition $\mathbb X_n$ in $S_1, S_2, \dots, S_k$ with associated $x_{S_i}\in S_i$ to minimize \[\sum_{i=1}^k\sum_{x\in S_i}d(x, x_{S_i})\] - Dimensionality reduction.
Multi-dimensional scaling (MDS) aims to find a projection $p:(\mathbb X_n, d)\to (\mathbb R^k, d_E)$ that minimizes \[\sum_{i\neq j=1,\dots,n} d(x_i,x_j)-d_E\big(p(x_i), p(x_j)\big)\]



The metric structure
$(\mathbb X_n, d)$ metric space.- Clustering.
$K$-medoids method aims to partition $\mathbb X_n$ in $S_1, S_2, \dots, S_k$ with associated $x_{S_i}\in S_i$ to minimize \[\sum_{i=1}^k\sum_{x\in S_i}d(x, x_{S_i})\] - Dimensionality reduction.
Multi-dimensional scaling (MDS) aims to find a projection $p:(\mathbb X_n, d)\to (\mathbb R^k, d_E)$ that minimizes \[\sum_{i\neq j=1,\dots,n} d(x_i,x_j)-d_E\big(p(x_i), p(x_j)\big)\] - Persistent homology
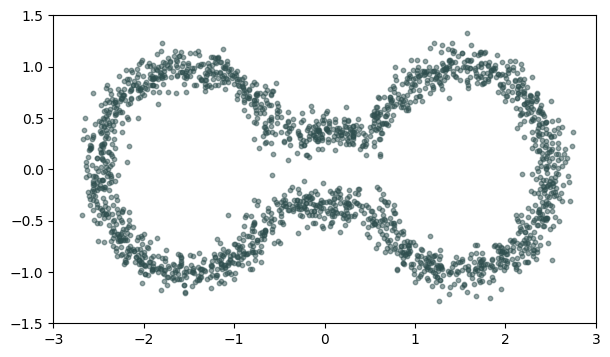
Filtration from the metric structure. The $k$-simplices of the Vietoris-Rips complex $VR_\epsilon(\mathbb X_n)$ are \[\{x_0, \dots, x_k\}\subseteq \mathbb X_n ~\text{ s.t. }~d(x_i, x_j)\leq \epsilon ~~~\forall i\neq j.\]
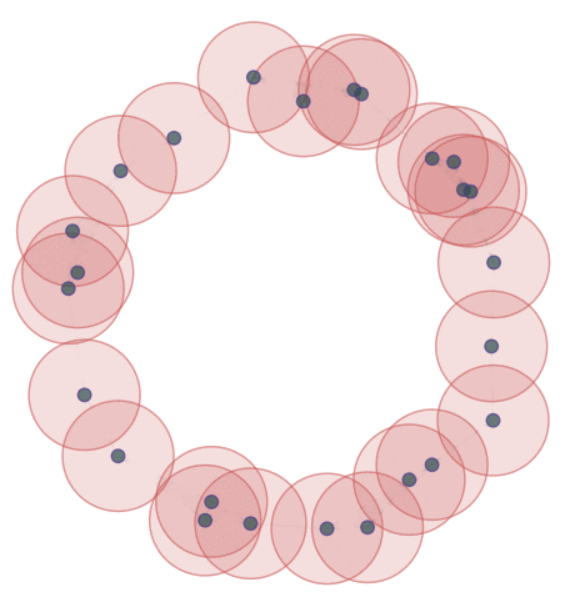
Persistent homology in a nutshell
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Q: How to infer the homology of $X$ from $\mathbb{X}_n$?
Point cloud
$\mathbb{X}_n \subset \mathbb{R}^D$

Evolving thickenings

Persistent homology in a nutshell
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Q: How to infer topological properties of $X$ from $\mathbb{X}_n$?
Point cloud
$\mathbb{X}_n \subset \mathbb{R}^D$

Evolving thickenings

Filtration of simplicial complexes

Persistent homology in a nutshell
Let $X$ be a topological space and let $\mathbb{X}_n = \{x_1,...,x_n\}$ be a finite sample of $X$.
Q: How to infer topological properties of $X$ from $\mathbb{X}_n$?
Point cloud
$\mathbb{X}_n \subset \mathbb{R}^D$

Filtration of simplicial complexes

Persistence diagram

Persistent homology
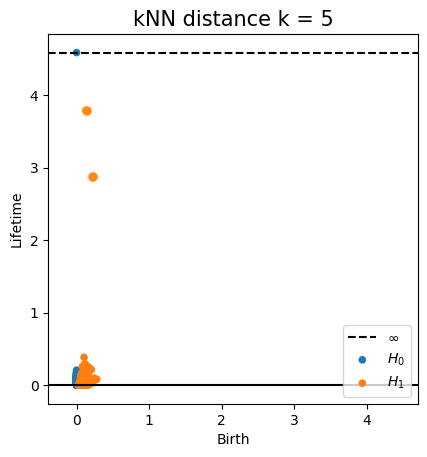
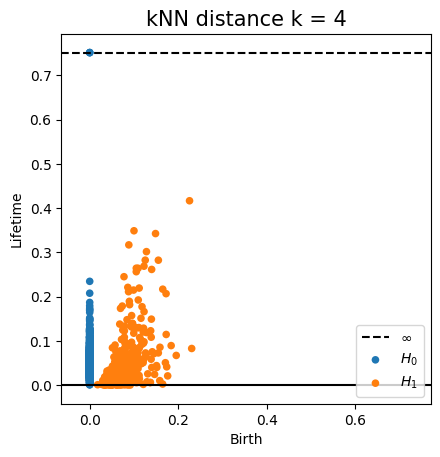
Metric space: $(\mathbb X_n, d_E)\sim (\mathcal M, d_E)$

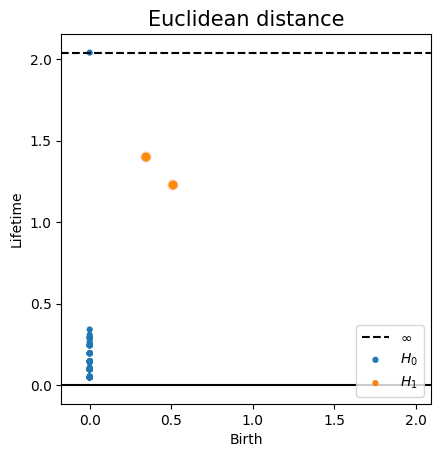
Persistent homology
Metric space: $(\mathbb X_n, d_{kNN})\sim (\mathcal M, d_\mathcal{M})~~~$(Bernstein, De Silva, Langford & Tenenbaum, 2000)


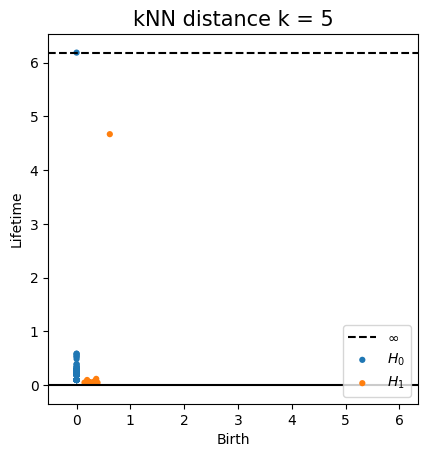
Persistent homology
Metric space: $(\mathbb X_n, d_{kNN})\sim (\mathcal M, d_\mathcal{M})$
Persistent homology
Metric space: $(\mathbb X_n, d_{kNN})\sim (\mathcal M, d_\mathcal{M})$


Persistent homology
Metric space: $(\mathbb X_n, d_{kNN})\sim (\mathcal M, d_\mathcal{M})$

The metric structure
Desired properties of a metric:$\checkmark$ 'Independence' on the ambient space (intrinsic).
$\checkmark$ Robustness to noise/outliers.
Density-based metric learning
Density-based metric learning
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ be a finite sample.

Density-based metric learning
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ be a finite sample.
Assume that:
- $\mathbb{X}_n$ is a sample of a compact manifold $\mathcal M$ of dimension $d$.
- The points are sampled according to a density $f\colon \mathcal M\to \mathbb R$.

Density-based metric learning



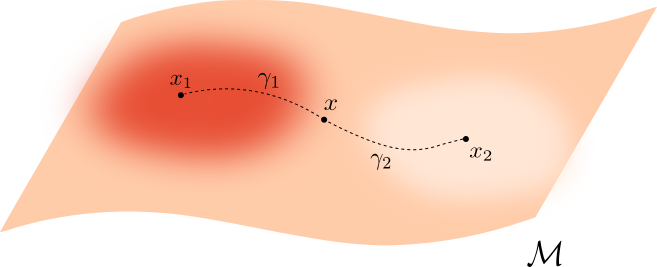
Fermat principle
The path taken by a ray between two given points is the path that can be traversed in the least time.
That is, it is the extreme of the functional \[ \gamma\mapsto \int_{0}^1\eta(\gamma_t)||\dot{\gamma}_t|| dt \] with $\eta$ is the refraction index.

Density-based geometry
(Hwang, Damelin & Hero, 2016)
Let $\mathcal M \subseteq \mathbb{R}^D$ be a manifold and let $f\colon\mathcal{M}\to \mathbb{R}_{>0}$ be a smooth density.
For $q>0$, the deformed Riemannian distance* in $\mathcal{M}$ is \[d_{f,q}(x,y) = \inf_{\gamma} \int_{I}\frac{1}{f(\gamma_t)^{q}}||\dot{\gamma}_t|| dt \] over all $\gamma:I\to \mathcal{M}$ with $\gamma(0) = x$ and $\gamma(1)=y$.
* Here, if $g$ is the inherited Riemannian tensor, then $d_{f,q}$ is the Riemannian distance induced by $g_q= f^{-2q} g$.
Fermat distance
(Mckenzie & Damelin, 2019) (Groisman, Jonckheere & Sapienza, 2022)
Let $\mathbb{X}_n = \{x_1,...,x_n\}\subseteq \mathbb{R}^D$ be a finite sample.
For $p> 1$, the Fermat distance between $x,y\in \mathbb{R}^D$ is defined by \[ d_{\mathbb{X}_n, p}(x,y) = \inf_{\gamma} \sum_{i=0}^{r}|x_{i+1}-x_i|^{p} \] over all paths $\gamma=(x_0, \dots, x_{r+1})$ of finite length with $x_0=x$, $x_{r+1} = y$ and $\{x_1, x_2, \dots, x_{r}\}\subseteq \mathbb{X}_n$.

Fermat distance

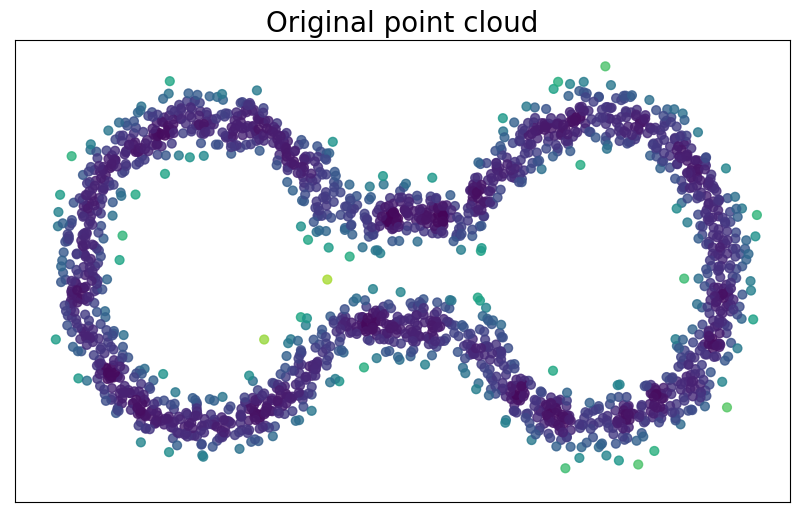
Fermat distance


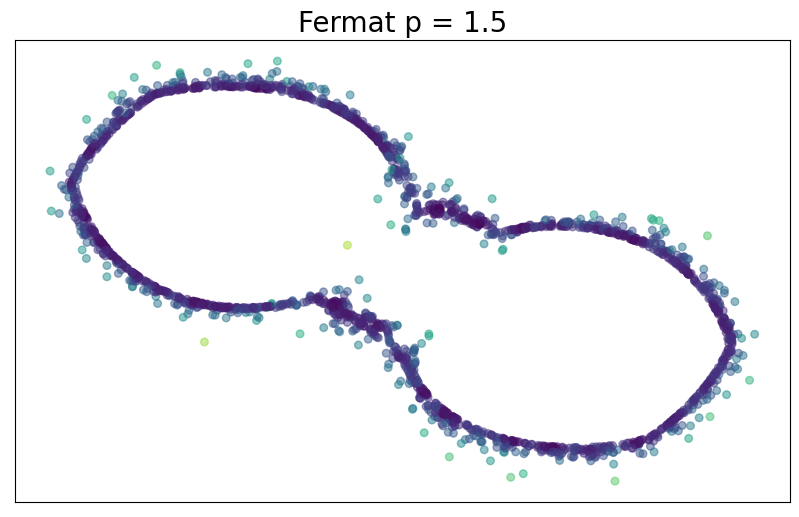
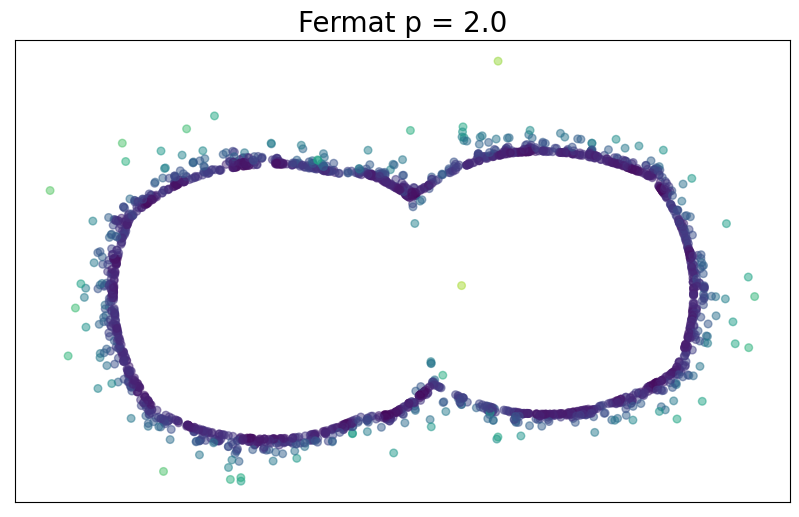
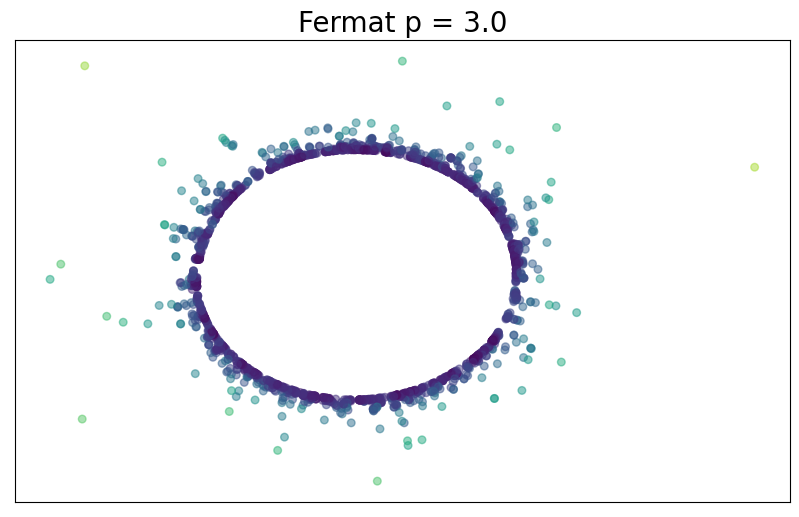
Convergence results
$d_{\mathbb X_n, p}$ is an estimator of $d_{f,q}$ if $q=(p-1)/d$.
Convergence results
Previous work
Set $q = (p-1)/d.$
- (Hwang, Damelin & Hero, 2016) If $L_{\mathbb X_n, p}(x,y) := \inf_{\gamma}\sum_{i=0}^{k}d_{\mathcal M}(x_{i+1},x_i)^{p}$ over all paths $\gamma=(x_0, \dots, x_{r+1})$ of finite length with $x_0=x$, $x_{r+1} = y$ and $\{x_1, \dots, x_r\}\subseteq \mathbb{X}_n$, then \[C(n,p,d) L_{\mathbb{X}_n,p}\underset{n \to \infty}{\overset{a.s}{\rightrightarrows}}d_{f,q}~~~ \text{ in } \{(x,y)\in \mathcal{M}: d_{\mathcal M}(x,y)\geq b\}.\]
- (Groisman, Jonckheere & Sapienza, 2022) If there exists $S\subseteq \mathbb{R}^d$ an open connected set and $\phi:S \to \mathbb{R}^D$ an isometric transformation such that $\phi(\bar S)=\mathcal{M}.$ \[ \lim_{n\to +\infty} C(n,p,d) d_{\mathbb{X}_n, p}(x,y) = d_{f,q}(x,y )~ \text{almost surely.}\]
Convergence results
(F., Borghini, Mindlin & Groisman, 2023)
Let $\mathcal{M}$ be a closed smooth $d$-dimensional manifold embedded in $\mathbb{R}^D$.
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]
Recall that \[d_{H}\big((X, d)(Y,d)\big) = \max \big\{\sup_{x\in X}d(x,Y), \sup_{y\in Y}d(X,y)\big\}, ~~\text{for }X,Y\subseteq (Z,d)\] \[d_{GH}\big((X, d_X),(Y,d_Y)\big)= \inf_{\substack{Z \text{ metric space}\\ f:X\to Z, g:Y\to Z \text{ isometries}}}d_H(f(X), g(Y))\]

Convergence results
(F., Borghini, Mindlin & Groisman, 2023)
Let $\mathcal{M}$ be a closed smooth $d$-dimensional manifold embedded in $\mathbb{R}^D$.
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]
Theorem (F., Borghini, Mindlin, Groisman, 2023)
Let $\mathbb{X}_n$ be a sample of a closed manifold $\mathcal M$ of dimension $d$, drawn according to a density $f\colon \mathcal M\to \mathbb R$.
Given $p>1$ and $q=(p-1)/d$, there exists a constant $\mu = \mu(p,d)$ such that for every $\lambda \in \big((p-1)/pd, 1/d\big)$ and $\varepsilon>0$ there exist $\theta>0$ satisfying
\[
\mathbb{P}\left( d_{GH}\left(\big(\mathcal{M}, d_{f,q}\big), \big(\mathbb{X}_n, {\scriptstyle \frac{n^{q}}{\mu}} d_{\mathbb{X}_n, p}\big)\right) > \varepsilon \right) \leq \exp{\left(-\theta n^{(1 - \lambda d) /(d+2p)}\right)}
\]
for $n$ large enough.
Fermat-distance
Computational implementation
- Complexity:
$O(n^3)$
reducible to $O(n^2*k*\log(n))$ using the $k$-NN-graph (for $k = O(\log n)$ the geodesics belong to the $k$-NN graph with high probability).
- Python library:
fermat
- Computational experiments:
ximenafernandez/intrinsicPH
Applications
Persistent homology
Convergence of persistence diagrams
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]
+Stability \[d_B\Big( \mathrm{dgm}\big(\mathrm{Filt}(X, d_X)\big), \mathrm{dgm}\big(\mathrm{Filt}(Y, d_Y\big)\Big)\leq 2 d_{GH}\big((X,d_X),(Y,d_Y)\big)\]
Convergence of persistence diagrams
\[\big(\mathbb{X}_n, C(n,p,d) d_{\mathbb{X}_n,p})\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ~~~ \text{ for } q = (p-1)/d\]
+Stability \[d_B\Big( \mathrm{dgm}\big(\mathrm{Filt}(\mathbb X_n, C(n,p,d) d_{\mathbb{X}_n,p})\big), \mathrm{dgm}\big(\mathrm{Filt}(\mathcal M, d_{f,q})\big)\Big)\leq 2 d_{GH}\big((\mathbb X_n,C(n,p,d) d_{\mathbb{X}_n,p}),(\mathcal M,d_{f,q})\big)\]
$\Downarrow$\[\mathrm{dgm}(\mathrm{Filt}(\mathbb{X}_n, {C(n,p,d)} d_{\mathbb{X}_n,p}))\xrightarrow[n\to \infty]{B}\mathrm{dgm}(\mathrm{Filt}(\mathcal{M}, d_{f,q})) ~~~ \text{ for } q = (p-1)/d\]
Fermat-based persistence diagrams

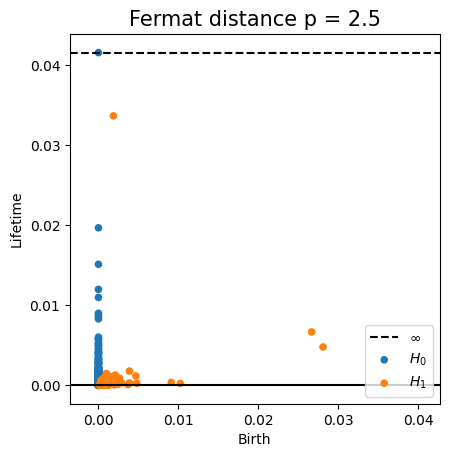
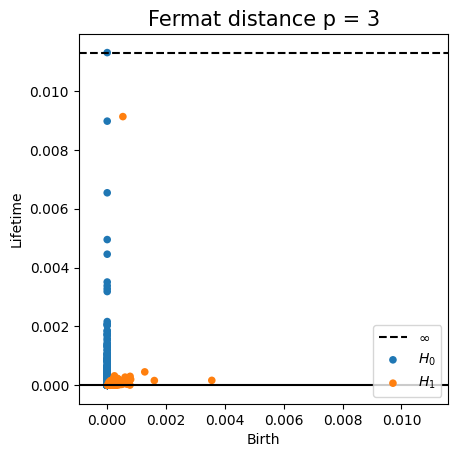
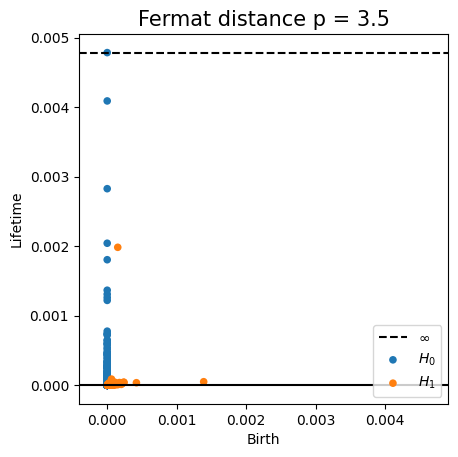
Fermat-based persistence diagrams


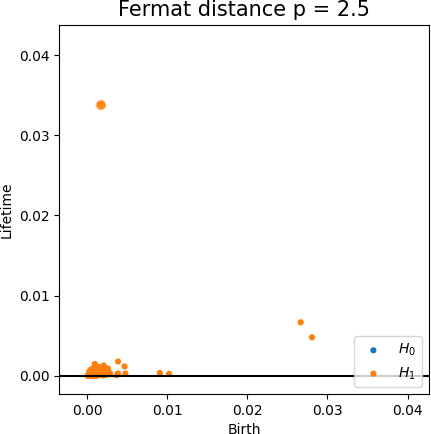
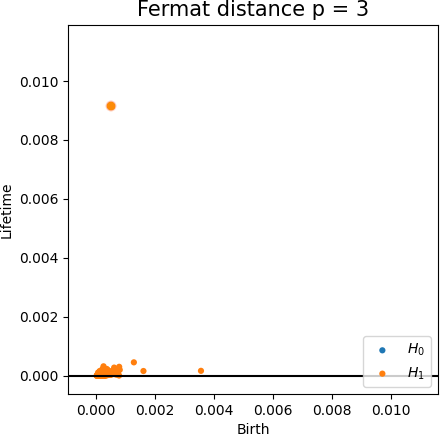
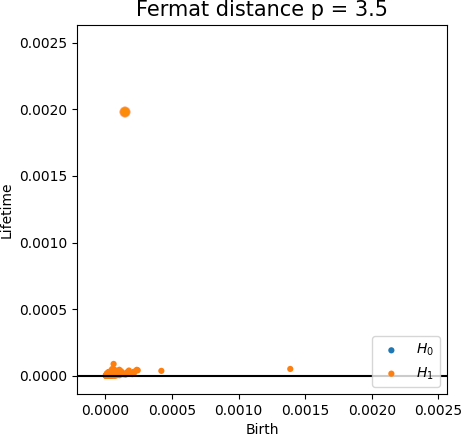
Fermat-based persistence diagrams


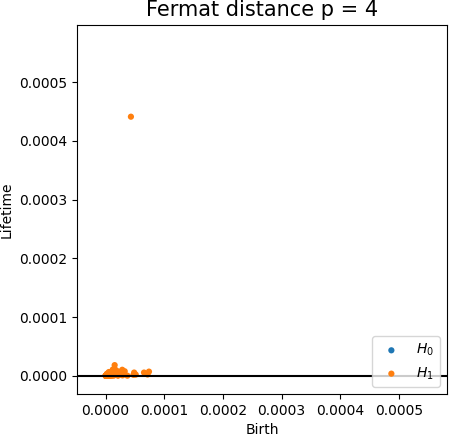
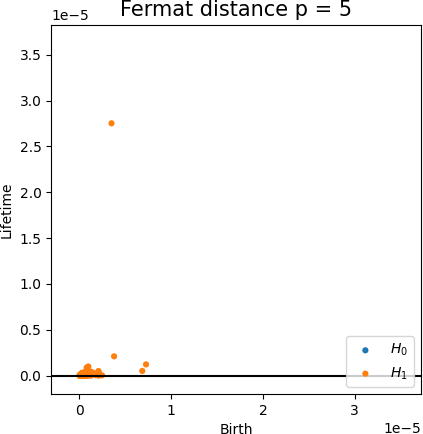
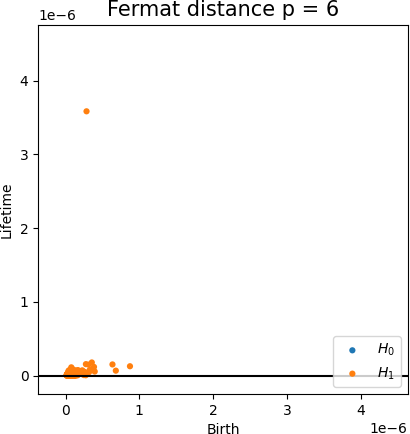
Fermat-based persistence diagrams
Intrinsic reconstruction





Fermat-based persistence diagrams
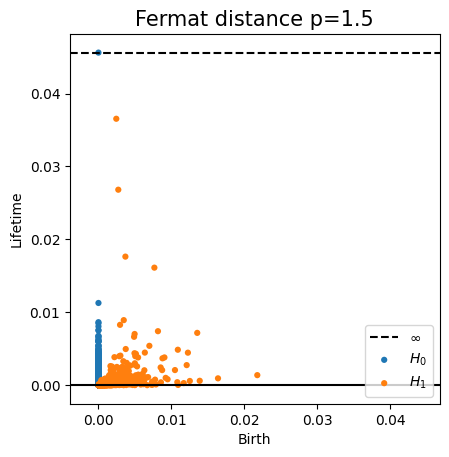
Robustness to outliers
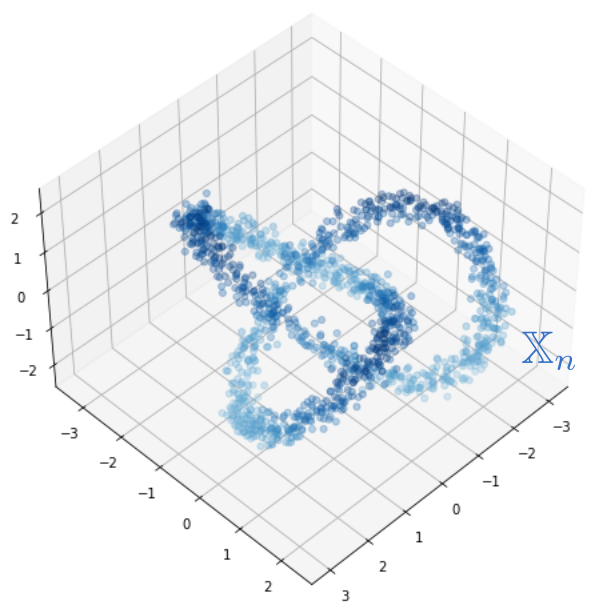
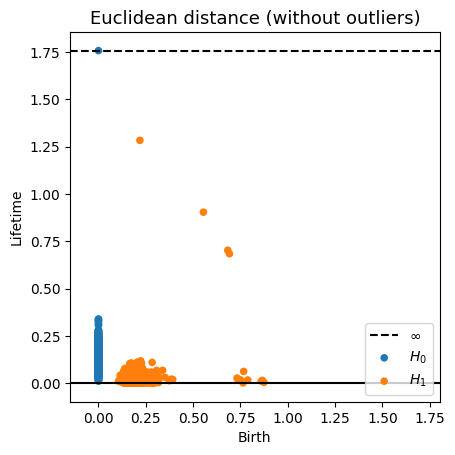
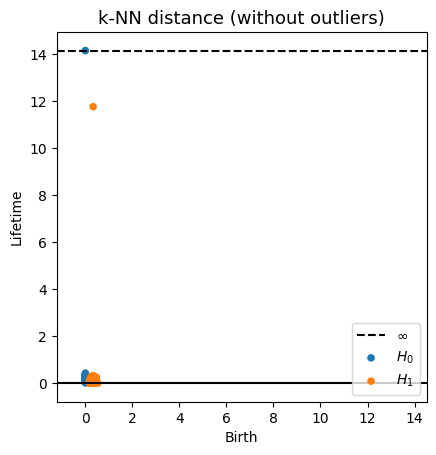
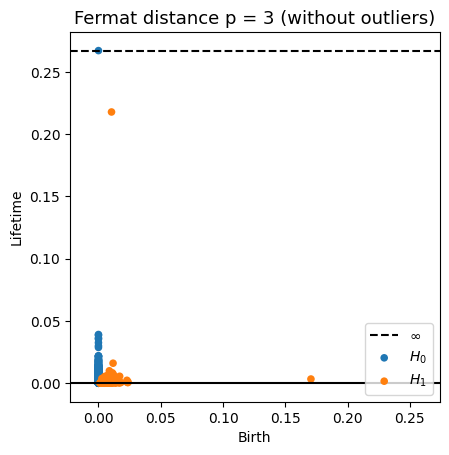
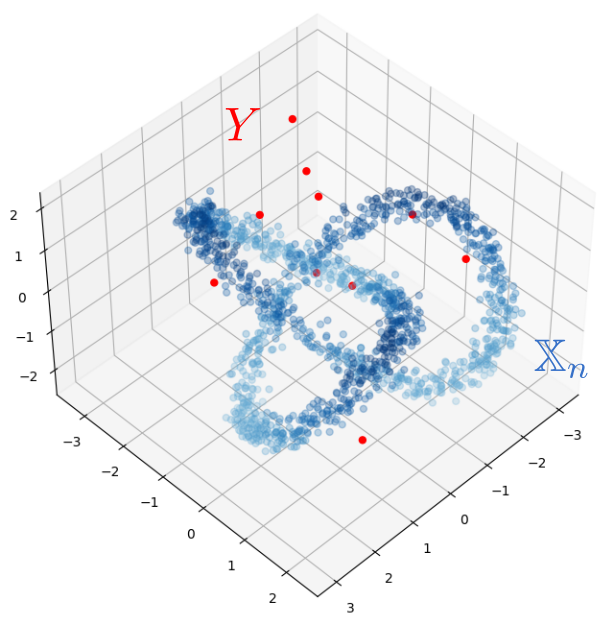
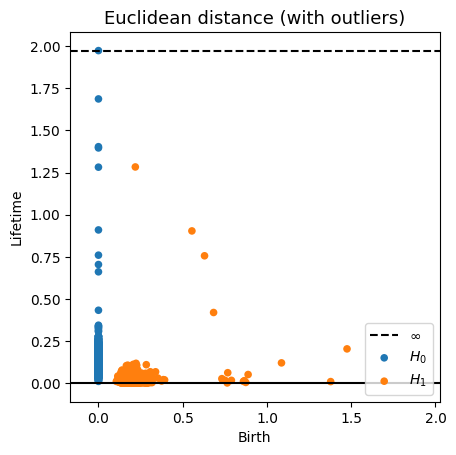
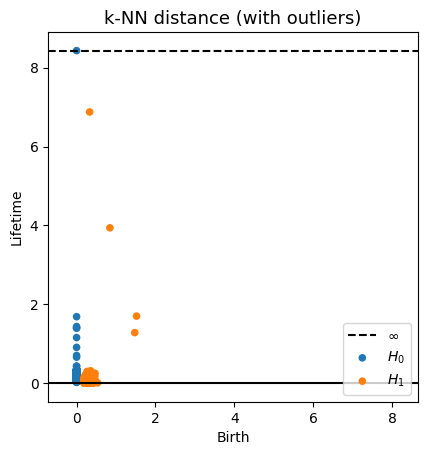
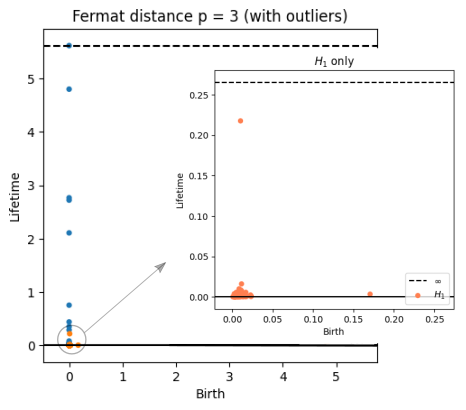
Fermat-based persistence diagrams
Robustness to outliers
Prop (F., Borghini, Mindlin, Groisman, 2023)
Let $\mathbb{X}_n$ be a sample of $\mathcal{M}$ and let $Y\subseteq \mathbb{R}^D\smallsetminus \mathcal{M}$ be a finite set of outliers.
Let $\delta = \displaystyle \min\Big\{\min_{y\in Y} d_E(y, Y\smallsetminus \{y\}), ~d_E(\mathbb X_n, Y)\Big\}$.
Then, for all $k>0$ and $p>1$,
\[
\mathrm{dgm}_k(\mathrm{Rips}_{<\delta^p}(\mathbb{X}_n \cup Y, d_{\mathbb{X}_n\cup Y, p})) = \mathrm{dgm}_k(\mathrm{Rips}_{<\delta^p}(\mathbb{X}_n, d_{\mathbb{X}_n, p}))
\]
where $\mathrm{Rips}_{<\delta^p}$ stands for the Rips filtration up to parameter $\delta^{p}$ and $\mathrm{dgm}_k$ for the persistent homology of deg $k$.

Time series Analysis
Anomaly detection
Electrocardiogram
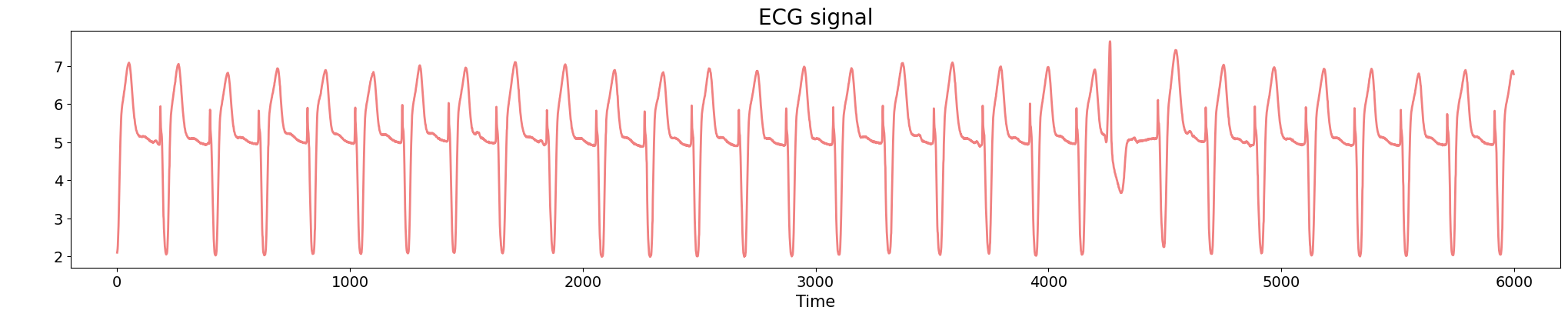
Source data: PhysioNet Database https://physionet.org/about/database/
Anomaly detection
Electrocardiogram

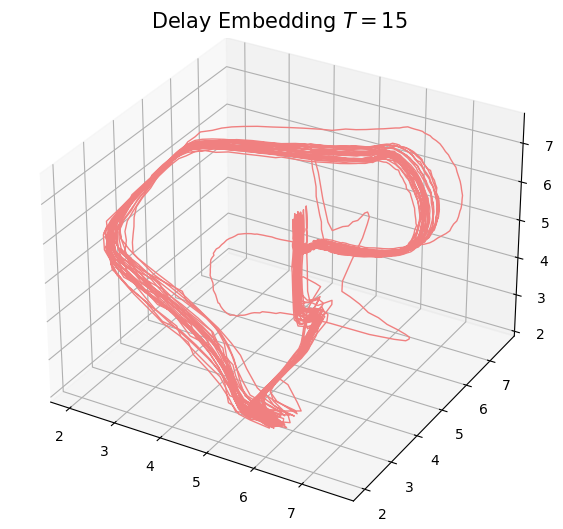
Anomaly detection
Electrocardiogram
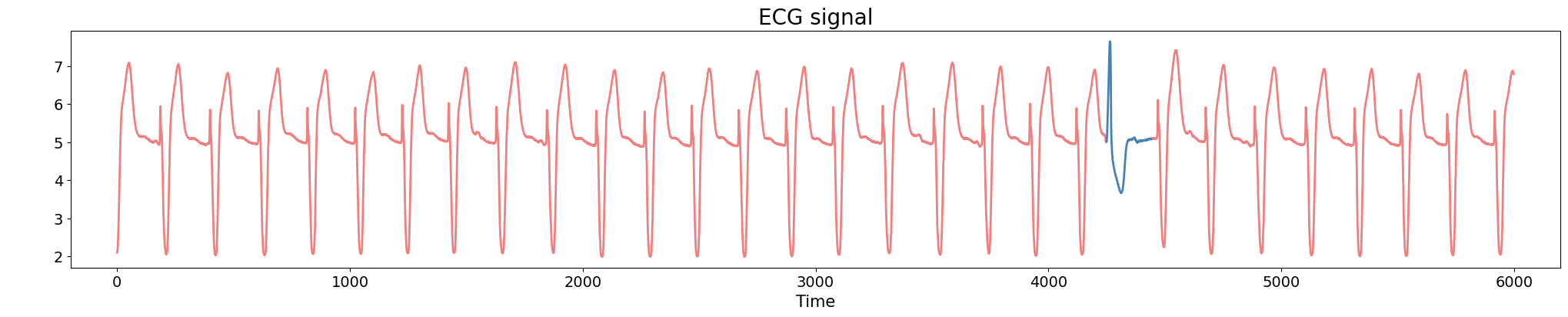
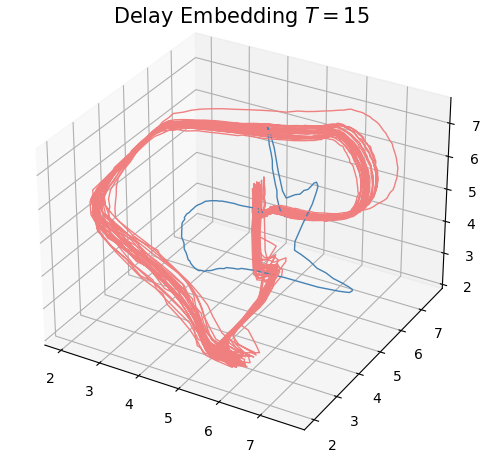
Anomaly detection
Electrocardiogram


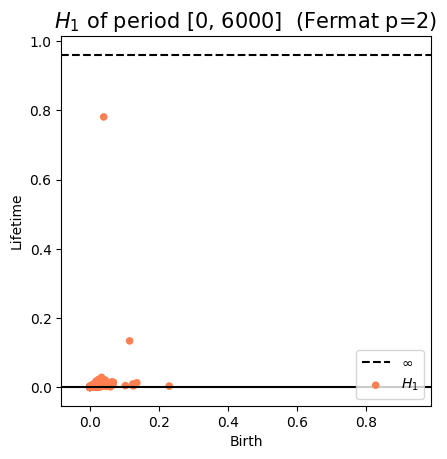
Anomaly detection
Electrocardiogram
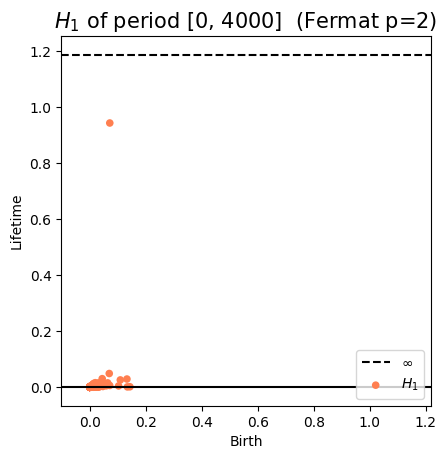
 \[t\mapsto \mathcal{D}_t\]
Approximate Derivative: $\dfrac{d_{B}(\mathcal{D}_t, \mathcal{D}_{t-\varepsilon})}{\varepsilon}$
\[t\mapsto \mathcal{D}_t\]
Approximate Derivative: $\dfrac{d_{B}(\mathcal{D}_t, \mathcal{D}_{t-\varepsilon})}{\varepsilon}$

Change-points detection
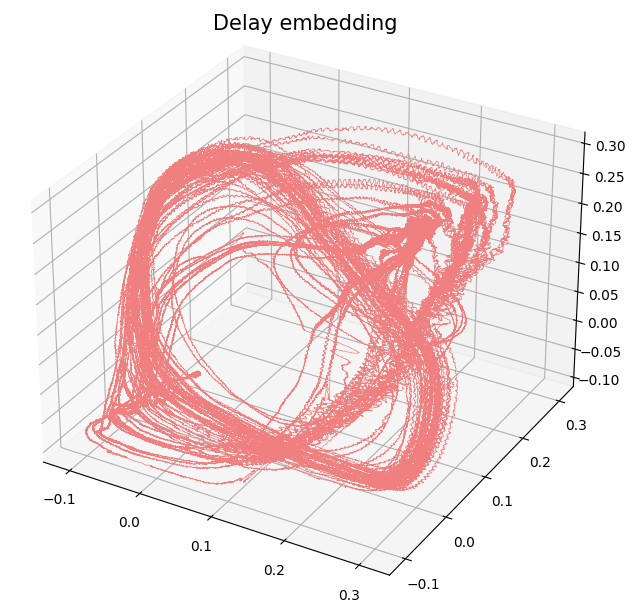
Birdsongs

Source data: Private experiments. Laboratory of Dynamical Systems, University of Buenos Aires.
Change-points detection
Birdsongs

Change-points detection
Birdsongs


Change-points detection
Birdsongs

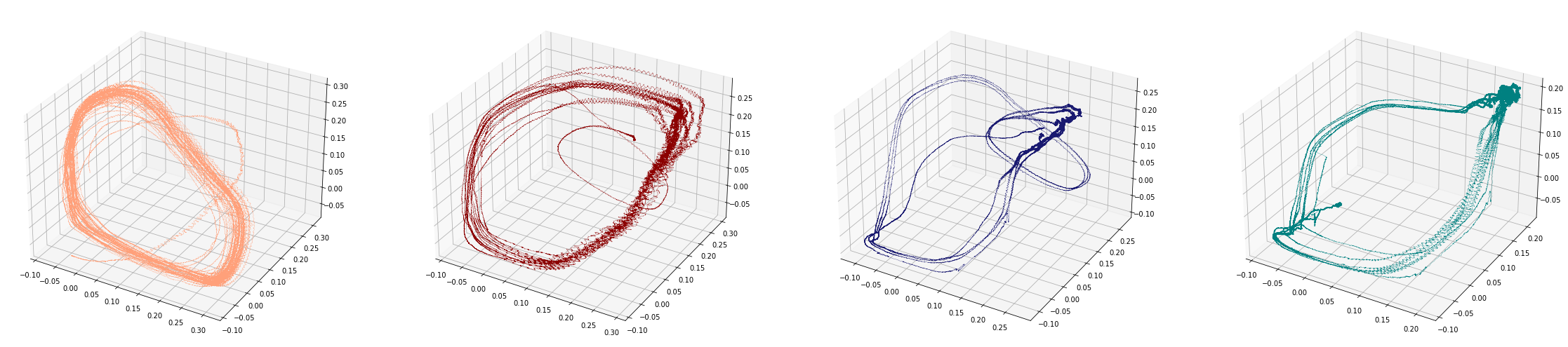

Change-points detection
Birdsongs


Future work
- Results in the noisy case
If $\widetilde{\mathbb{X}}_n = \{\widetilde {x}_1, \widetilde {x}_2, \dots, \widetilde {x}_n\} $ such that $\widetilde{x}_i = x_i + \xi_i $ with $x_i \in \mathcal M$ and $\xi_i\in \mathbb R^D$ 'noise', \[\big(\mathbb{\widetilde X}_n, C(n,p,d) d_{\mathbb{\widetilde X}_n,p}\big)\xrightarrow[n\to \infty]{GH}\big(\mathcal{M}, d_{f,q}\big) ?\] - Density-based homology theory
Given $X$ a topological space and $\mu:X\to \mathbb R$ a density, 'understand' the homology of $(X,\mu)$.

References
- Source: X. Fernandez, E. Borghini, G. Mindlin, P. Groisman. Intrinsic persistent homology via density-based metric learning. Journal of Machine Learning Research 24(75):1−42 (2023).
- Github Repository: ximenafernandez/intrinsicPH
- Tutorial: Intrinsic persistent homology. AATRN Youtube Channel (2021)
- Python Library: fermat